前置: 05-BayesNetwork, 06-BayesInference, 07-Probabilistic
Markov Decision Process
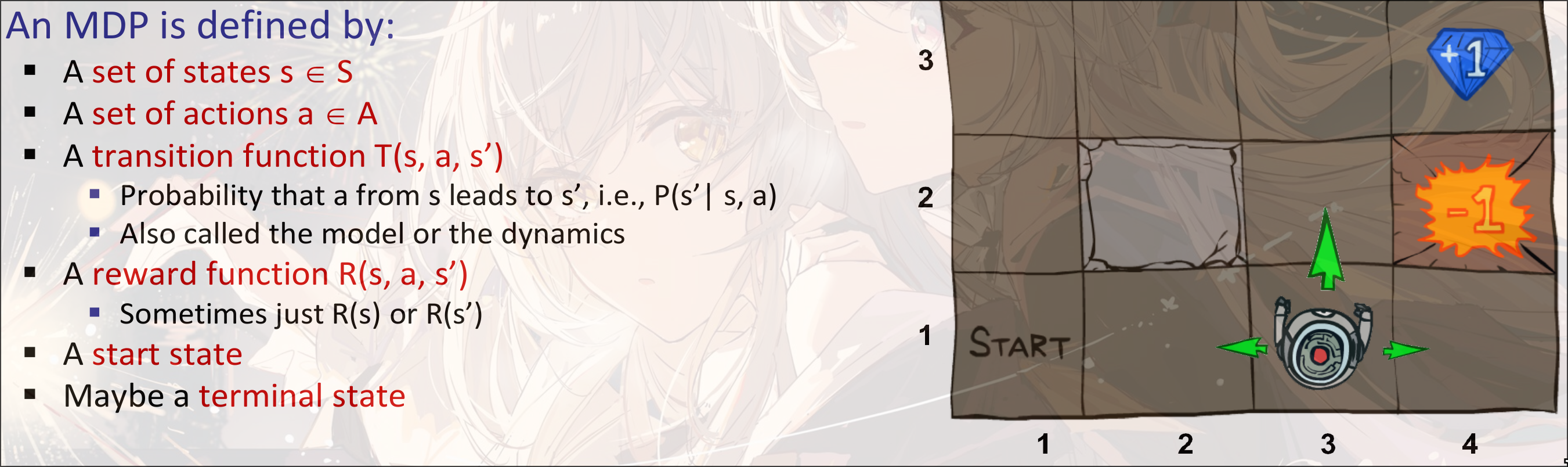
是Non-deterministic的搜索算法
假定了下一时刻的状态只和当前事态的状态和当前时刻的action有关, 与之前的状态和动作无关
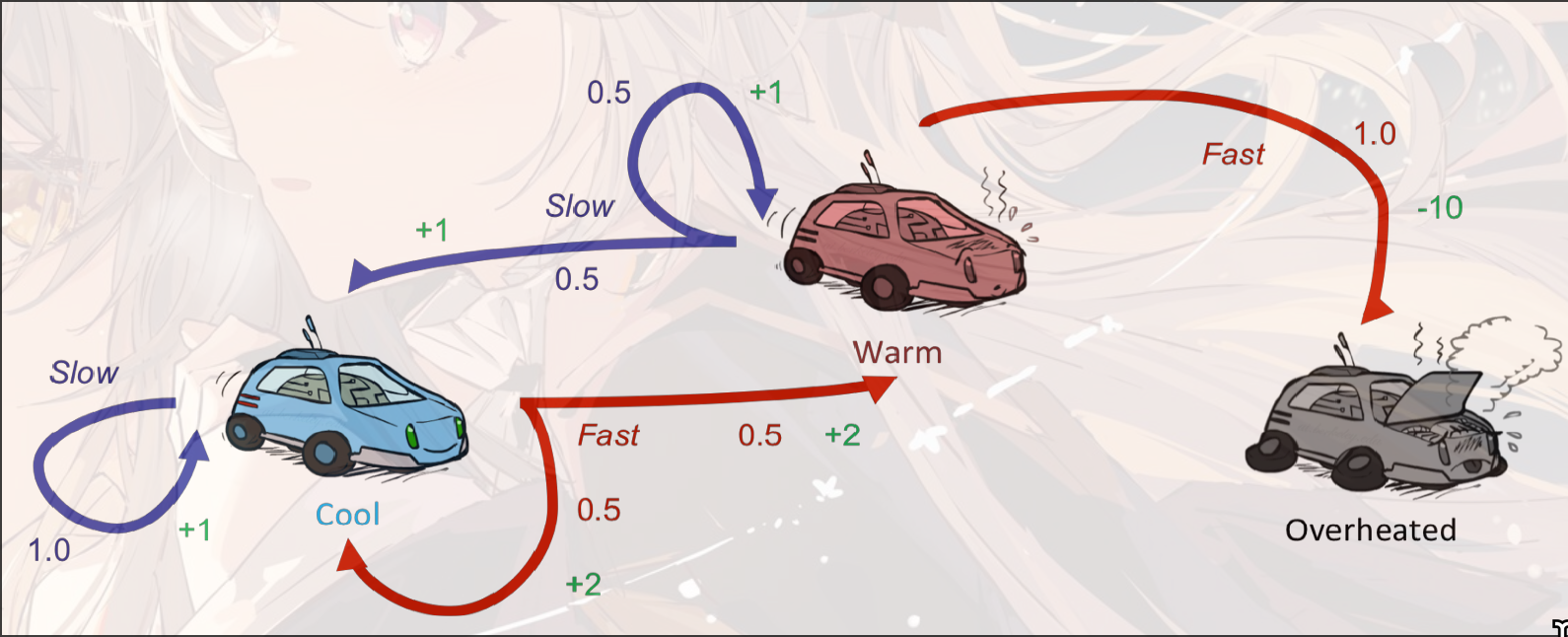
假设是reward function, 表示每存活一定时间对总的reward的更新:
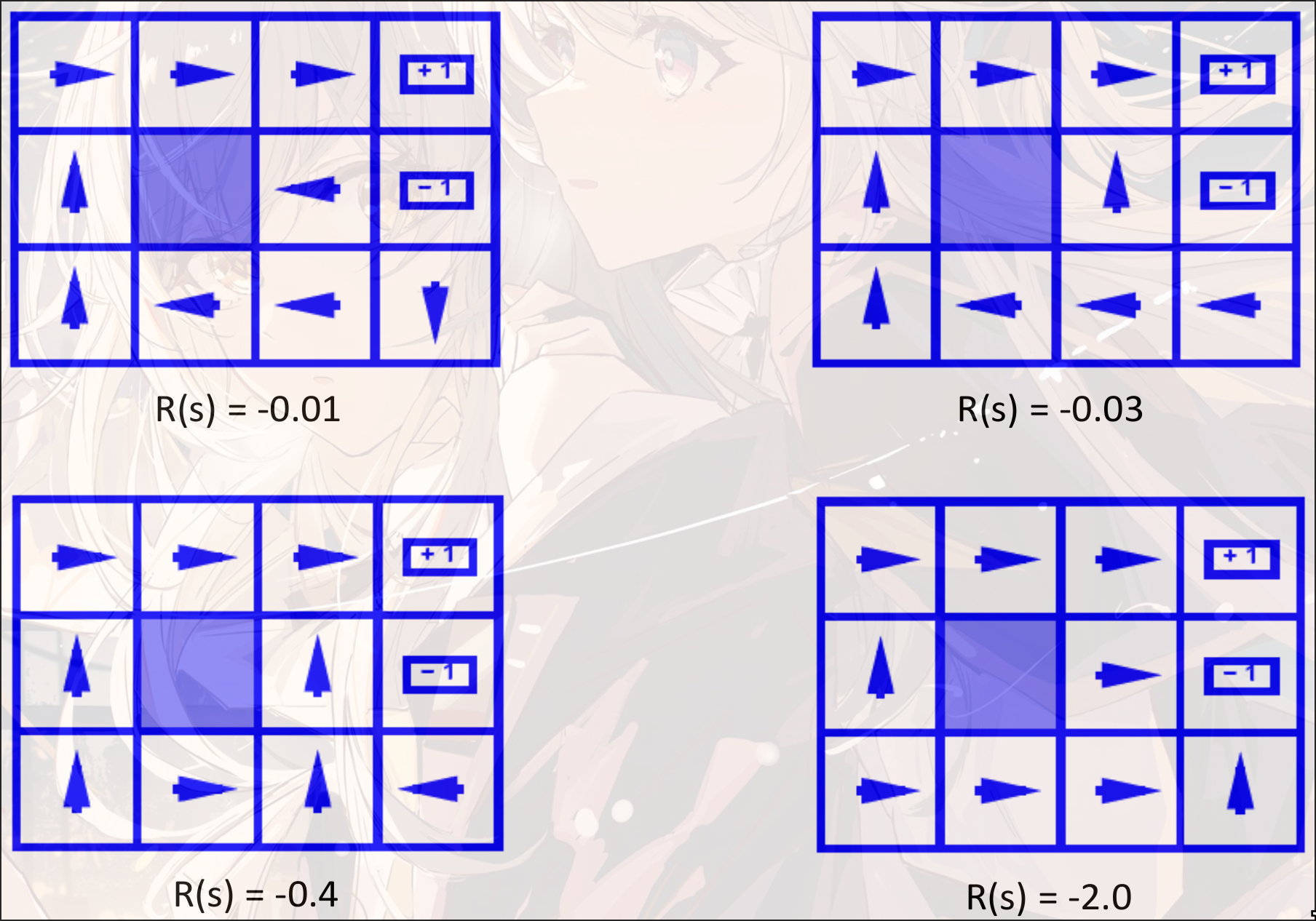
不同的reward function会导致不同的结果
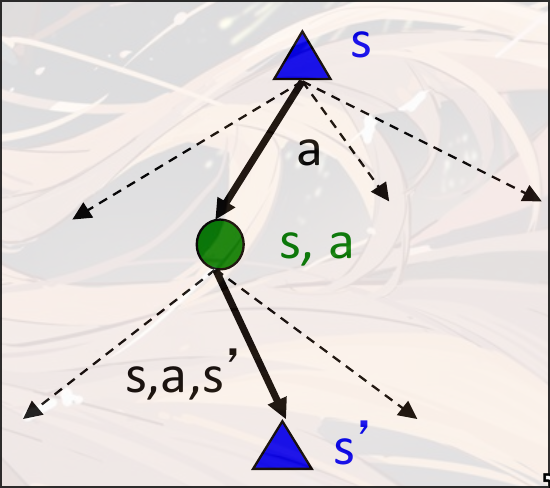
Markov Search Tree
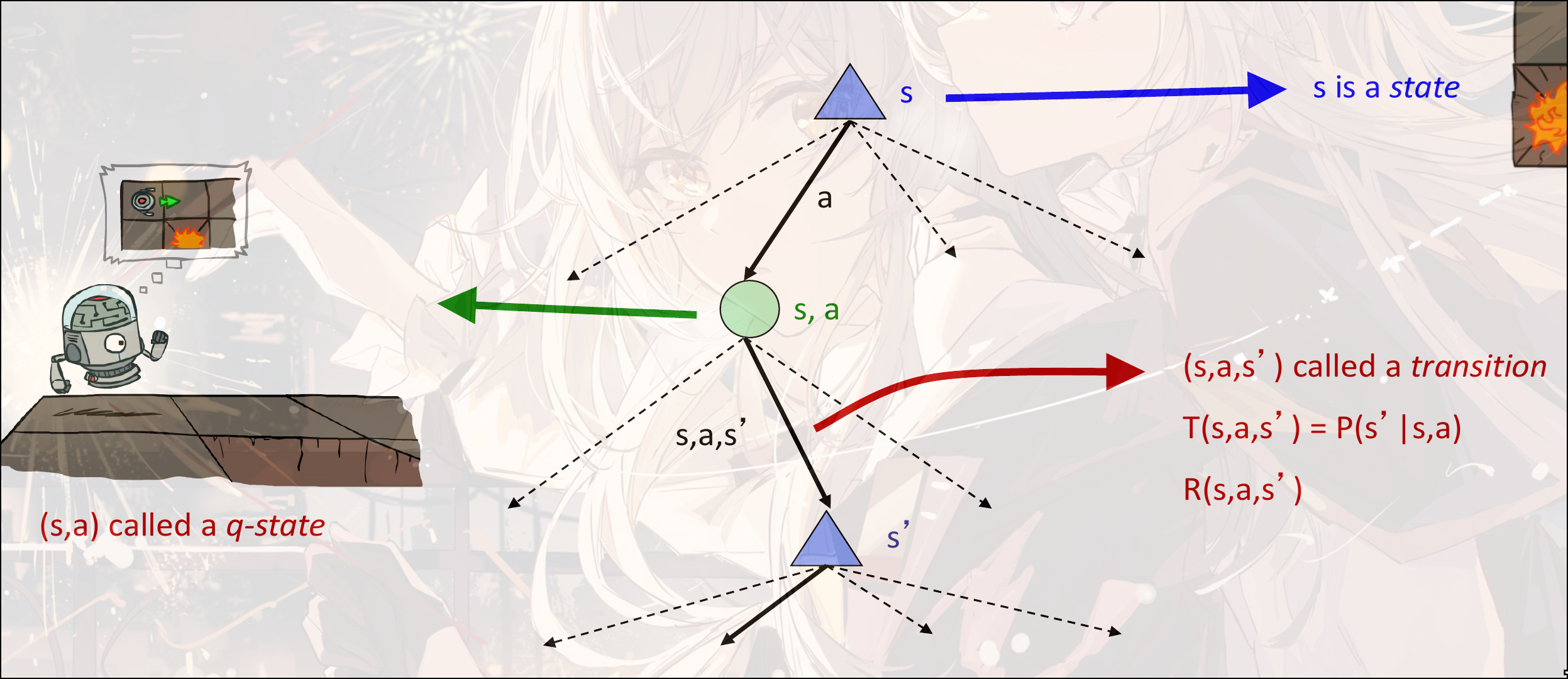
节点并不是真实的节点, 而是虚拟的节点, 类似expectation-max的节点
Utilities of Sequences
如何考虑未来的reward的影响? 应该放弃眼前的收益考虑更长远的收益还是更期待长期的收益?
Utility Function: 是基于整个Sequence的值的函数, 并不完全等于Reward Function. 如果只关注了最近的一个值的update, 那么就是Reward
Discounting: 如果未来的reward比较低, 对当前的影响不大, 那么设置一个discounting factor: , 每一个时间步的reward的影响(reward的值)乘上作为未来的权重. 如果更看重当前, 那么设置, 如果更看中未来, 可以让.
有助于防止无限循环, 有助于算法收敛
防止无限循环的方法:
- 设置discounting factor<1
- 设置最多轮数, 设置最大搜索深度
- 设置aborting state. 如果一个状态进去就出不来, 就设置这个状态为停止状态, 表示这个状态没必要再搜索
Optimal Quantities
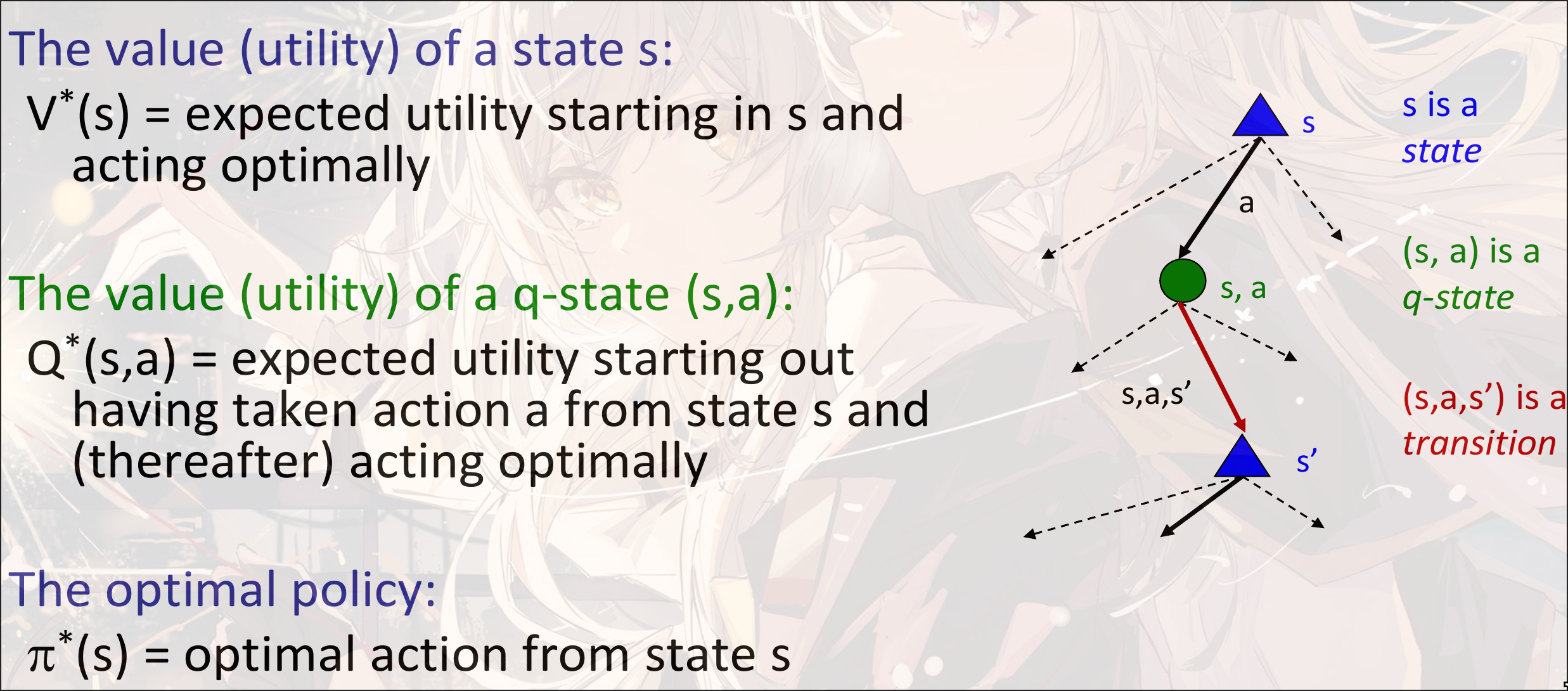
optimal value function:
其中, 是状态转移的概率, 是状态转移的reward, 是discounting factor.
前面两个式子可以写成一个总式(最后一行), 叫做Bellman Equation
Value Iteration
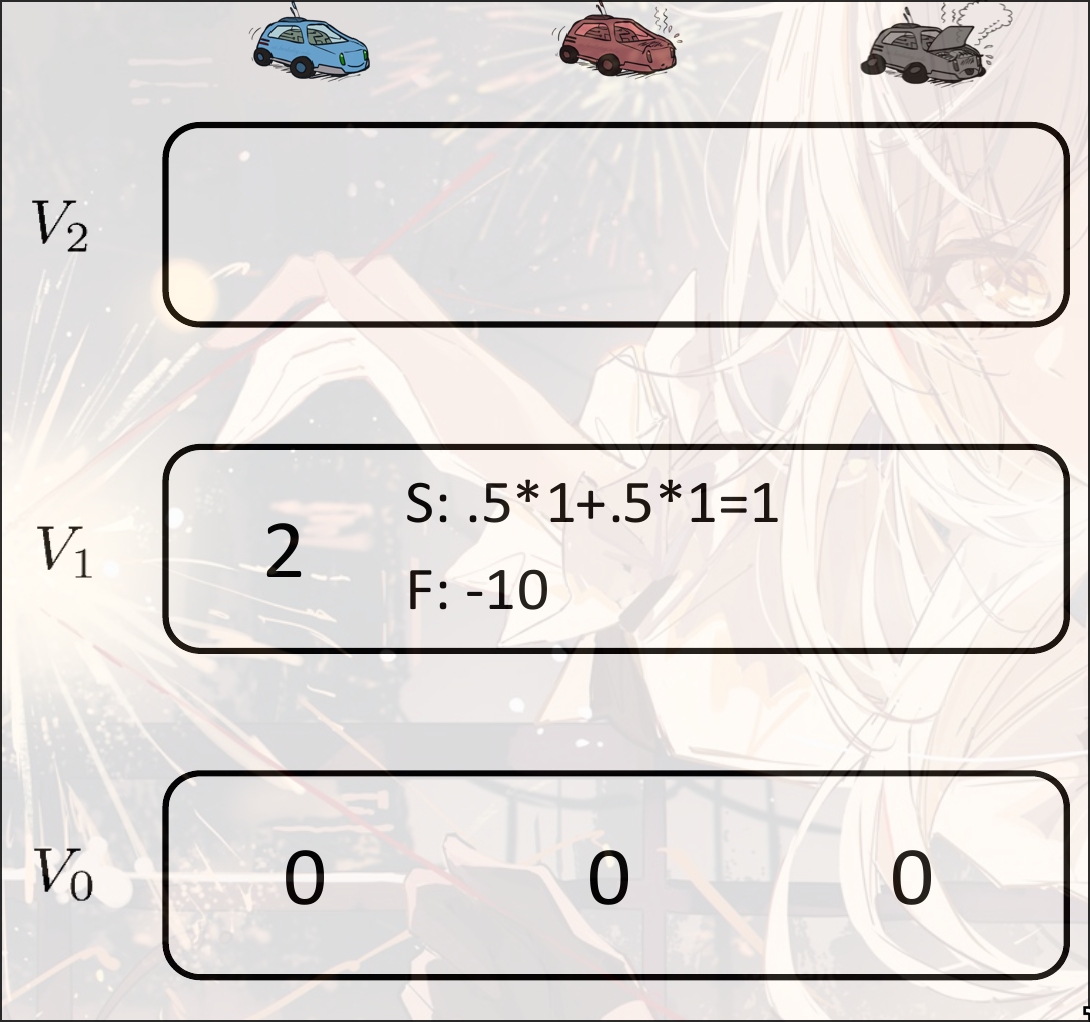
从开始, 迭代计算
复杂度:
Q-value
相同的, Q-value也可以使用Value Iteration计算
proof
Bellman equation
max norm
the bellman update is a contraction by a factor of on the space of utility vectors
there exists only one optimal value of contraction transformation
Value iteration converges to
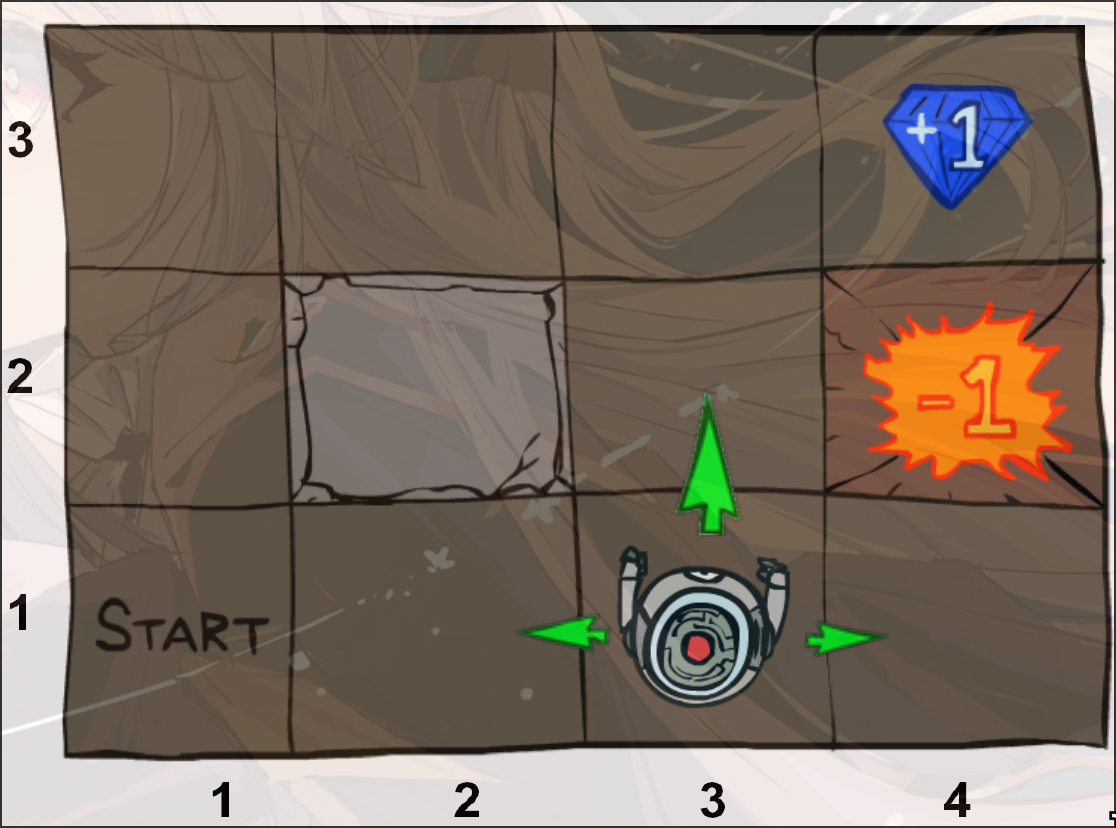
example
Example
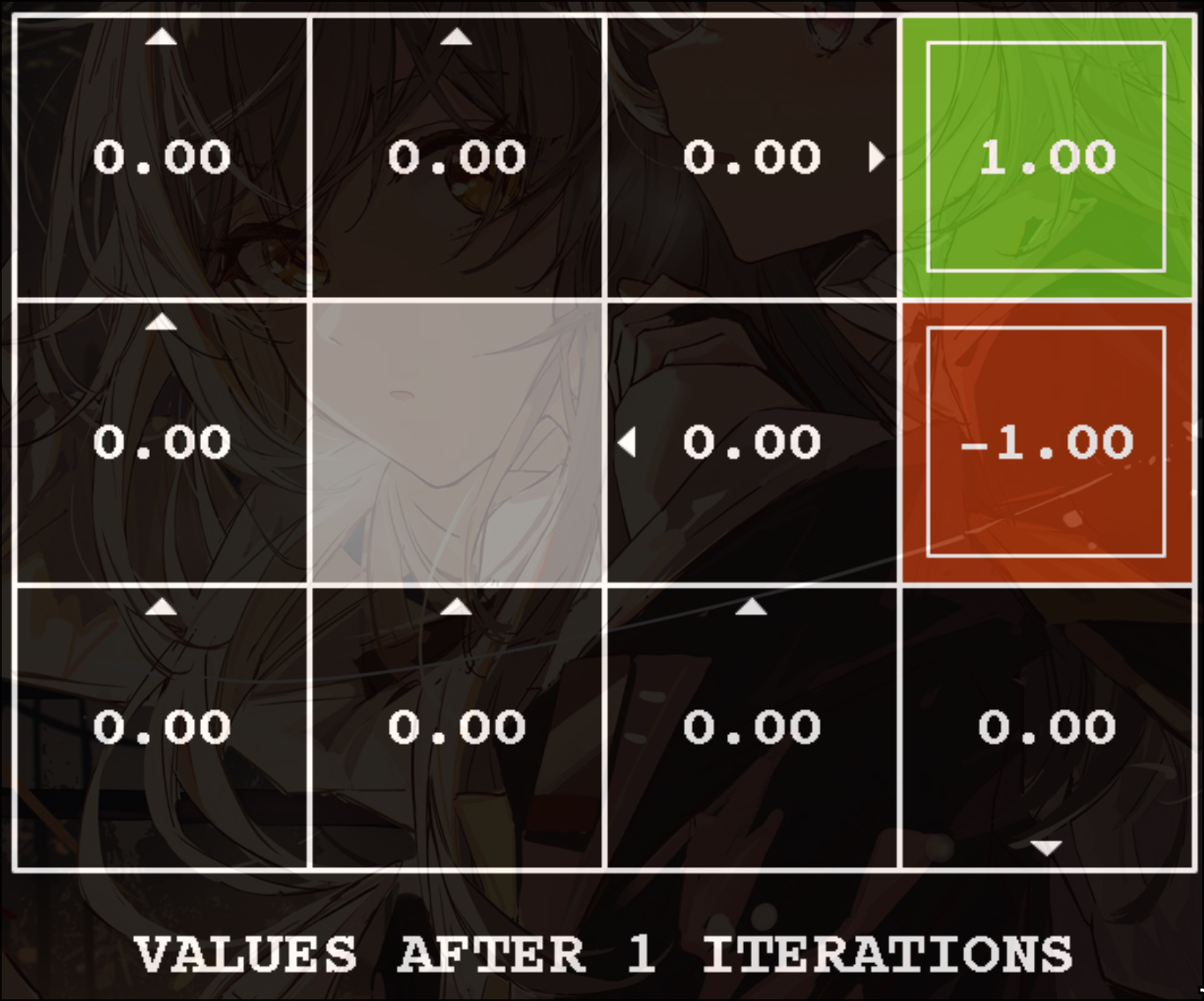
Value Iteration:
Example
Value Iteration:
Computing action from values
称作policy extraction
或者如果已知optimal q-function, 可以写成:
相较于从value得出, action从q-value得出更容易(计算量更少)
Policy Iteration
Problem with Value Iteration:
- 太慢, 每一次迭代的时间复杂度为
- 对自己的所有值域遍历(每个值对应的value都更新, 复杂度),
- 取每个action中的最大值()
- 每个action的值由action对应状态的转移概率和对应的Reward乘积决定()
- 在max这一步的value基本没有改变
因此提出: 只关注即可, 而不是关注每一个值
-
计算当前Policy的结果
计算一个固定的(不一定optimal, 可能是随机)Utility Function
-
优化Policy
更新policy使用one-step look-ahead, 可能不是最优, 但是收敛速度更快
-
Step1
不再提供action, 而是给定一个policy函数, 根据这个函数计算对应的值.
复杂度:
或者假定已经达到了收敛状态, 那么只需要解出一个线性方程即可
-
Step2
更新Policy:
Value Iteration v.s. Policy Iteration
都是计算相同的内容: 计算一个最优的action
都是动态规划
Value Iteration:
- 每一次更新都会计算所有的state的value
- 会track所有的state的值
Policy Iteration:
- 只更新一部分固定的state. 每一个iteration都只关注一个state而不是全部的state
- 每一次计算之后都会更新policy function
- 可能收敛更快