09-RL

前置: 08-MDP

Reinforcement Learning

所有的 RL tag的文章均基于此

使用类似MDP的定义, 但是这个时候并不清楚$T$或者$R$

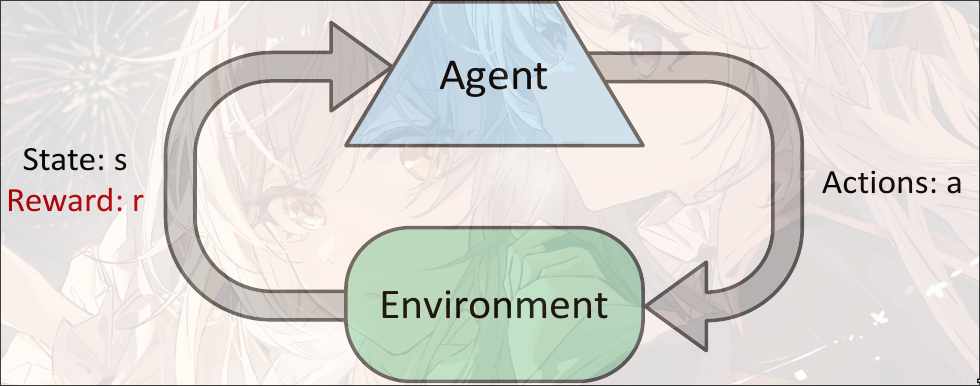
在Agent中存在$\pi$或者说action, 在environment中存在state, reward function和transition function.

认为在environment中的作为ground truth, 因此是function而不是model(model是Agent中学习到的)

Basic Idea: 假设在时间步$t$有一个策略${\pi }_{\omega }(s_t)$,

• 找到当前可观测状态$s_t$
• 找到action: $a={\pi }_{\omega }(s_t)$
• 根据environment的transition probability $T(s_{t+1},a_t,s_t)$找到$s_{t+1}$
• 我们的目标是最大化$R={\mathbb{E}}_{\pi }\left[{\sum }_{t=0}^{T-1}{r}_t(s_t,a_t)\right]$

Offline learning v.s. Online learning:

offline不需要真正运行一次游戏, 不会对环境产生影响(e.g. MPD)

online需要真实运行一次游戏, 对环境影响(e.g. RL)

Model Based Learning

通过经验进行学习一个近似的模型, 然后将学习到的模型进行估计

Step 1: 采取不同的action然后基于outcomes计算MDP Model

• 计算outcomes $s^{\prime }$根据给定的$s,a$

  a是由${\pi }_i(s)$给出的, 这个${\pi }_i$是在Agent中, 我们认为在更新environment的过程中, ${\pi }_i$是固定的.

• 归一化, 然后计算$\hat{T}(s,a,s^{\prime })$

  我们认为虽然$T$的parameters中有$s,a,s^{\prime }$三个, 但是$s$是current state是固定的, $a={\pi }_i(s)$认为是固定的. 因此随机性只产生在$s^{\prime }$处.

• 计算$R(s,a,s^{\prime })$对于每一个给定的$s,a,s^{\prime }$

  Reward Function是environment中的函数, 有可能是已知的, 但是在真实的environment中也是需要迭代的.

Step 2: 使用MDP的Iteration的方法计算, 更新${\pi }_{i+1}$

Pros:

• 更有效率地利用sample(低sample complexity)

Cons:

• May not scale to large state space

  • solving MDP is intractable for very large $|S|$

    当状态空间很大的时候, MDP很难搜索

• RL feedback loop tends to magnify small model errors

  本身RL就是一个模拟, 自带一定的误差. 多次训练可能会放大这个error

• Much harder when the environment is partially observable

  当空间是not perfect infomation的时候, 很难完整的看到environment

Model Free Learning

Note

model based v.s. model free

假设计算所有人的平均年龄:

• 如果已知每个年龄有多少概率: $$E[A]=\sum _{a}P(a)a$$
• 如果未知$P(a)$
  • model based $$\hat{P}(a)=\frac{\#a}{N}$$ $$E[A]\approx \sum _a\hat{P}(a)a$$
  • model free $$E[A]\approx \frac{1}{N}\sum _i{a}_i$$

区别: 是否要估计某一个统计量的分布. Model free是直接通过sample来模拟一个概率分布

passive v.s. active Reinforcement learning

• passive RL: 在根据过去已经给定的策略下估计, 常见在evaluation
• active RL: 在根据过去给定的策略, 并且手动去测试下估计

Passive RL

简单来说就是policy evaluation

• Input: a fixed policy $\pi (s)$
• don’t know $T(s,a,s^{\prime })$
• don’t know $R(s,a,s^{\prime })$
• goal: learn state values

Example

Direct Estimation

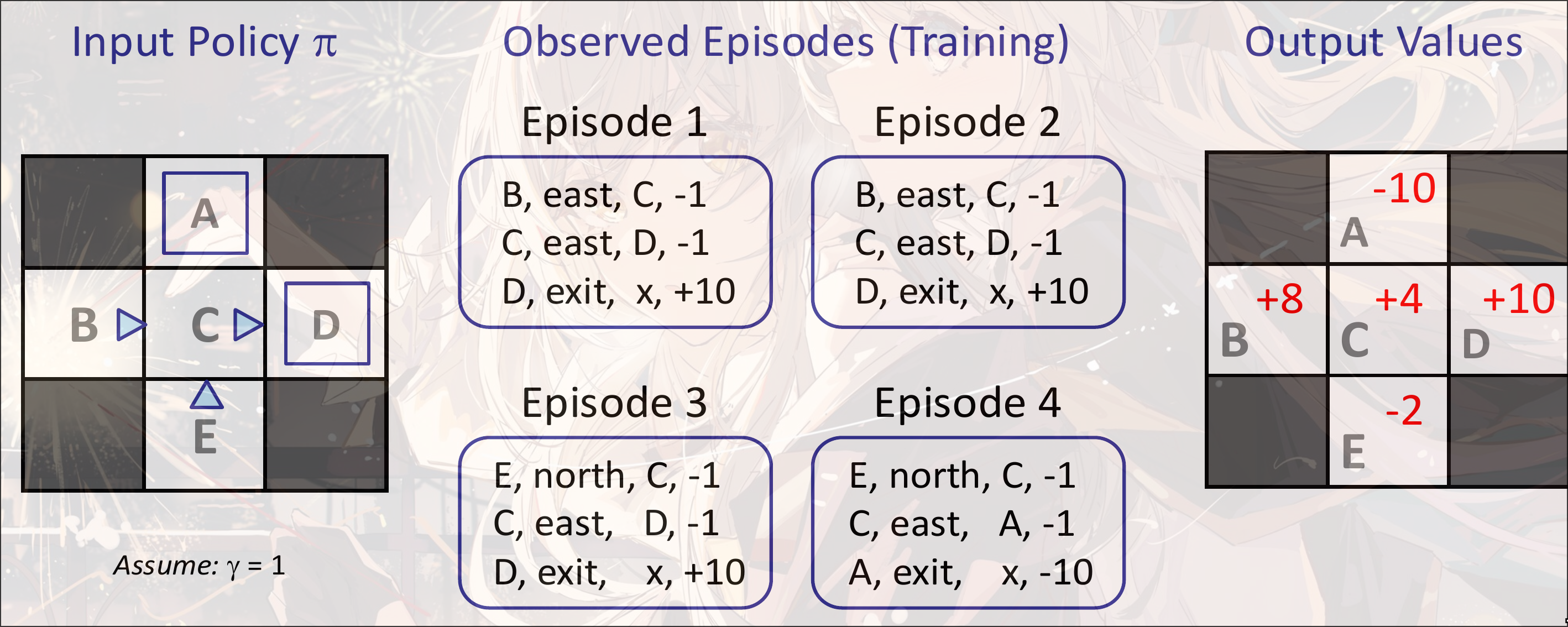
Goal: Compute each state value under $\pi$

Idea: Average together obversed samples values

对于B: 只有两个, 即Episode1, Eposide2, 加和的结果是(8+8)=16, Average=8

对于C: 我们只关心从C开始的, 四个Eposide都有C, 那么只看四个的最下面两个value: (-1+10)+(-1+10)+(-1+10)+(-1-10)=16, Average=4

对于A: 只有一个, Eposide4, -10

对于E: 两个, Eposide3,Eposide4, (-1-1+10)+(-1-1-10)=-4, Average=-2

Pros:

• 易于理解
• 不需要任何关于$R(s,a,s^{\prime })$和$T(s,a,s^{\prime })$的知识
• 使用sample transition能近似计算出来正确的结果

Cons:

• 浪费了state connection的信息, 每个state是独立的, 所以需要很长时间的学习

Sample-Based Policy Evaluation

给定一个固定的策略, state的value是一个期望: $V^{\pi }(s)={\sum }_{s^{\prime }}T(s,\pi (s),s^{\prime })[R(s,\pi (s),s^{\prime })+\gamma V^{\pi }(s^{\prime })]$

• Idea1: 使用真实采样去估计期望

  $sampl{e}_1=R(s.\pi (s),s_1^{\prime })+\gamma V^{\pi }(s_1^{\prime }))$

  $sampl{e}_2=R(s.\pi (s),s_1^{\prime })+\gamma V^{\pi }(s_1^{\prime }))$

  $V^{\pi }(s)\leftarrow \frac{1}{N}{\sum }_{i}sampl{e}_i$

  但是有一个问题: RL的过程中, 一旦采取了action, 那么environment一定会改变. 如果想要回到上一个状态, 那么需要走回上一个状态. 但是environment已经改变掉了, 因此是无法改变的

• Idea2: Update value of $s$ after each transition $s,a,s^{\prime },r$

  Update $V^{\pi }([3,1])$ based on $R([3,1],up,[3,2])$ and $\gamma V^{\pi }([3,2])$

  …

  有一个问题: 会在结果不精确的前提下flash掉之前的估计的结果. 因为这个是based on一个数据而不是大量数据的平均

• Idea3:

  Note

  在有增量的连续数据流的过程中, 如何维持一个average:

  记录之前的average和之前的数据量, 增量数据只需要${\mu }_{new}=\frac{{\mu }_{old}\times n+x_{new}}{n+1}$

  $\mathbb{E}[\mu ]$是$\mathbb{E}[x_i]$凸的combination, 因此是无偏的

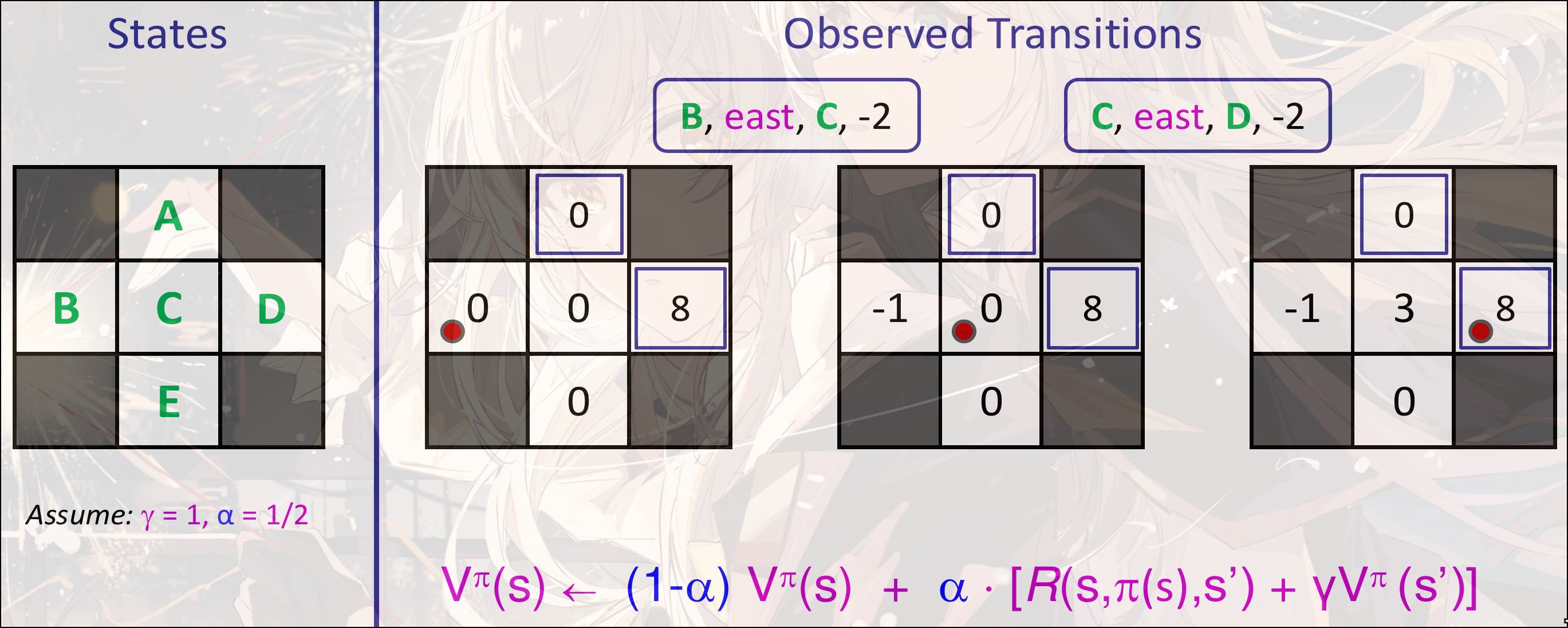
TD Learning

$$sample=R(s,\pi (s),s^{\prime })+\gamma V^{\pi }(s^{\prime })$$ $$V^{\pi }(s)\leftarrow (1-\alpha )V^{\pi }(s)+\alpha \times sample$$ $$\Rightarrow V^{\pi }(s)\leftarrow V^{\pi }(s)+\alpha \times (sample-V^{\pi }(s))$$

$\alpha$是learning rate. $sample-V^{\pi }(s)$是TD error

Example

第一个transition:

$$V^{\pi }(B)\leftarrow (1-\frac{1}{2})V^{\pi }(B)+\frac{1}{2}[R(B,\pi (B),C)+1\times V^{\pi }(C)]$$ $$=\frac{1}{2}\times 0+\frac{1}{2}\times (-2+0)=-1$$

第二个transition:

$$V^{\pi }(C)\leftarrow \frac{1}{2}{V}^{\pi }(C)+\frac{1}{2}[R(C,\pi (C),D)+1\times V^{\pi }(D)]$$ $$=\frac{1}{2}\times 0+\frac{1}{2}[-2+1\times 8]=3$$

TD Value Learning的优点:

• Model free
• Bellman Update with running sample mean

缺点:

• 需要tranisition model去imporve

Q-Learning

对Q-state进行TD Value learning:

$$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha \times [R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })]$$

我们直接从$Q(s,a)$中学习, 不需要转移模型

缺点: 空间复杂度会比较大. 每一个格子需要存储所有action的value

接受一个sample $s,a,s^{\prime },r$

根据旧的$Q(s,a)$来更新新的$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha [r(s,a,s^{\prime })+\gamma \times {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })]$

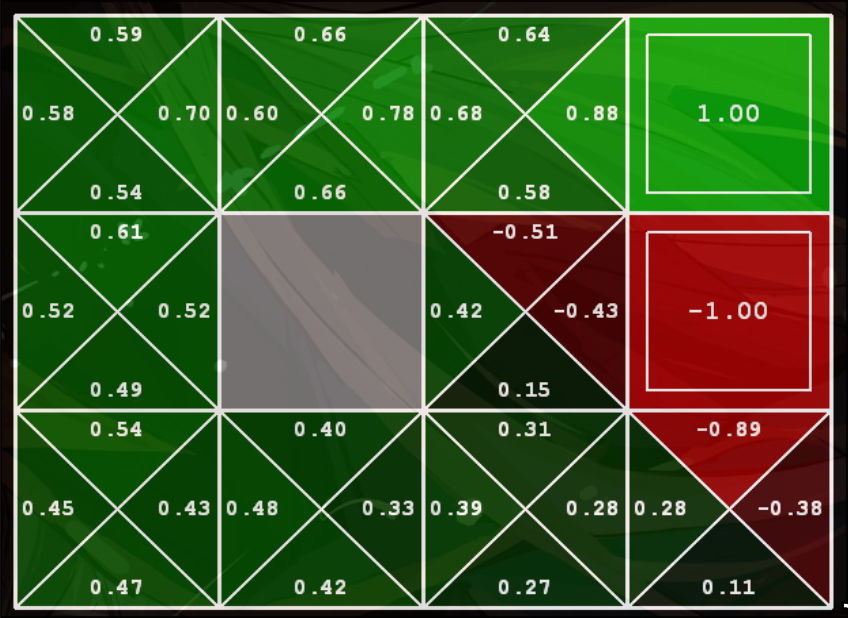
性质:

• 根据已有的policy $\pi$去更新value. 但是是和采样的policy是无关的. 是off-policy learning.

  但是需要更多探索, learning rate($\alpha$)不能太大

虽然TD value learning很像梯度下降, 但是并不是梯度下降, 是不动点迭代

Exploration and Exploitation

$\epsilon$-greedy

是一个Exploration的方法

每一个时间步, 根据概率$\epsilon$去选择: 随机行动($\epsilon$)或者根据现有概率行动($1-\epsilon$)

可能会做一些非常愚蠢的动作, 有些动作可以认为是重复无限次.

Optimisitic Exploration Functions

如果一个state value是$u$, 这个state经过了$n$次, 那么$f(u,n)=u+\frac{k}{\sqrt{n}}$

当探索次数比较小的时候, 这个state的function比较大, 会更倾向探索. 如果探索次数比较多, 会趋向于自己本身的value, 根据自己本身的value来选择action

$$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha \times [R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }f(Q(s^{\prime },a^{\prime }),n(s^{\prime },a^{\prime }))]$$