LESR

Paper

Introduce

问题: source state repr通常包含general的环境信息, 但是缺少关于当前任务的特定细节信息, 这些信息可能对value network的训练起到重要作用

使用LLM增强state的表达, 获取内在隐藏的表达, 增强value network从state到reward的准确性

提出LLM-Empowered State Representation(LESR), 利用LLM编码能力和对物理世界的解释能力来生成task-related state representation. 然后, LLM利用生成的state repr生成reward函数.

Method

Problem Statement

定义MDP为$(S,A,R,P,p_0,\gamma )$, 其中$P(s^{\prime }|s,a)$是转移函数, $p_0$是初始状态分布, $\gamma$是discount factor. 目标是学习一个RL policy $\pi (a|s)$, 最大化reward expectation: $Q_{\pi }(s_t,a_t)={\mathbb{E}}_{\pi }[{\sum }_{t=0}^{\infty }{\gamma }^t{r}_t|s_t,a_t]$

定义Lipschitz constant: 假设数据空间$\mathcal{X}\in {\mathbb{R}}^d$, 标签空间$\mathcal{Y}\in \mathbb{R}$. 有训练数据集${\mathcal{X}}_0\subset \mathcal{X}$, 其标签为${\mathcal{Y}}_0=\{y_i|y_i=u(x_i),x_i\in {\mathcal{X}}_0\}\subset \mathcal{Y}$, 其中$x_i$是基于概率分布$\rho$从${\mathcal{X}}_0$的采样, 函数$u:{\mathcal{X}}_0\subset \mathcal{X}\mapsto \mathcal{Y}$是一个映射Lipschitz constant, 该常数定义为: $$\text{Lip}(u,{\mathcal{X}}_0)={\sup }_{x_1,x_2\in {\mathcal{X}}_0}\frac{\Vert u(x_1)-u(x_2){\Vert }_2}{\Vert x_1-x_2{\Vert }_2}$$

LLM-Empowered Statement Representation

基于LLM嵌入的广泛的知识和先验信息, 使用LLM生成state repr.

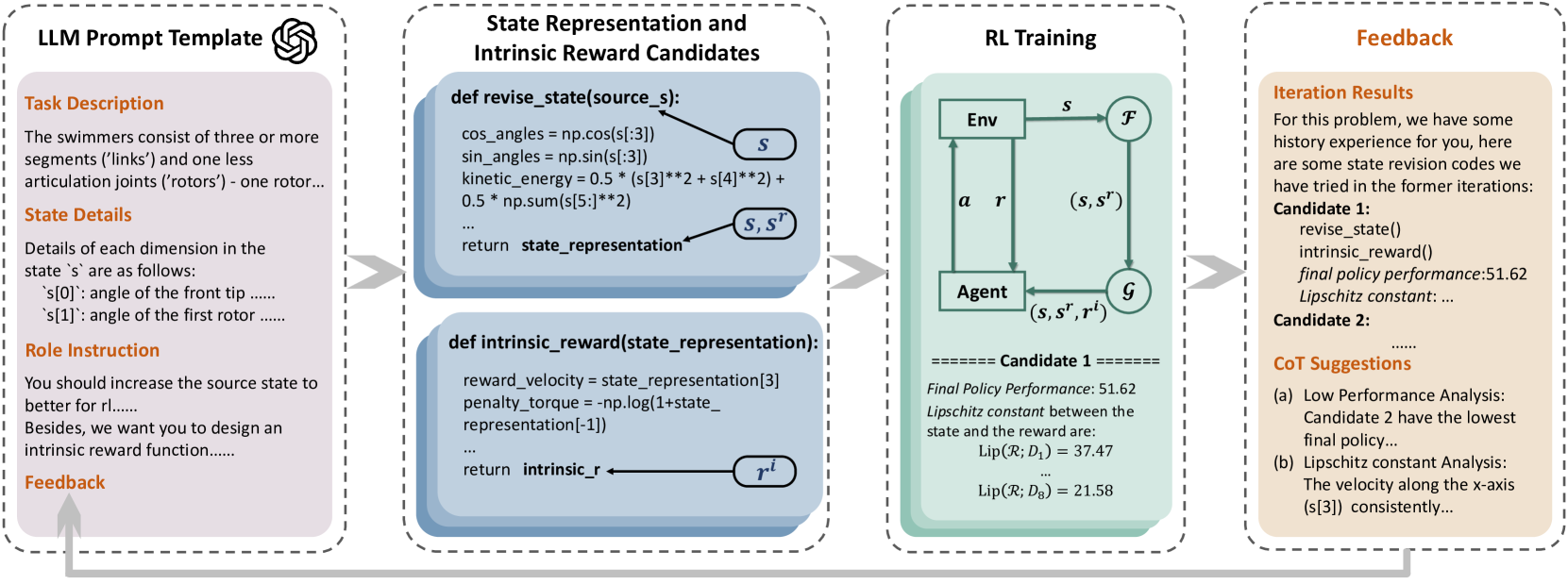
prompt输入分成4个部分:

1. Task Description: 当前任务的描述
2. State Details: 原始state的每一个维度所代表的含义
3. Role Instruction: 要求LLM生成任务相关的状态表达和intrinsic reward代码
4. Feedback: 历史信息

目标是通过LLM生成一个python函数$F$, 将原始空间的state($s_t$)映射到LLM-Empowered state representation($s_t^{\tau }$) space中. RL训练时, 显式将原始state和LLM-Empowered state拼接($s_t^c=(s_t,s_t^{\tau })$)作为observe variable.

生成$F$之后, 使用LLM基于函数$F$再次生成一个reward function $G$, 这个reward函数接收拼接后的$s_t^c$, 生成一个reward.

因此, 目标为

$$\underset{F,G}{\max }\underset{\pi }{\max }{\mathbb{E}}_{F,G,\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t(r+w\cdot r^i)|r^i=G\left(s_t,F(s_t)\right)\right]$$

Lipschitz Constant for Feedback

Explanation

Lipschitz constant表征一个函数的平滑性. 对于一个函数(映射)而言, 其Lipschitz constant计算方式为:

$$\text{Lip}(u,{\mathcal{X}}_0)=\underset{x_1,x_2\in {\mathcal{X}}_0}{\sup }\frac{\Vert u(x_1)-u(x_2){\Vert }_2}{\Vert x_1-x_2{\Vert }_2}$$

需要区分映射和Lipschitz常数.

为了增强状态表示的鲁棒性, 多次迭代query LLM, 包含先前的训练结果作为Feedback. 每个training iteration, 从LLM中采样K个state representation和intrinsic reward function code $F_k,G_k,k=1,\cdots ,K$. 然后在$N_{\text{small}}$时间步中同步进行K个训练, 用于评估$F_k,G_k$.

Continuous Extrinsic Reward Scenarios:

• 对于一条给定的轨迹 $T_i=\{s_t^C[i],r_t{\}}_{t=1}^H$, 其中$s_t^C[i]$表示$s_t^C$的第$i$维度
• 定义针对给定轨迹$T_i$的Lipshcitz constant array: $$C_k^T=[\text{Lip}(u_i;T_i){]}_{i=1}^{|S^C|}$$ 其中, $u_i$是将$s^C=(s,s^{\tau })$映射到extrinsic reward(不是上面提到的intrinsic reward)的一个函数. 每一个维度都有一个映射, 一共有$|S^C|$个. 因此$C_k^T\in {\mathbb{R}}^{|S^C|}$
• 使用$C_k^T$更新全局的$C_k$: $$C_k=\tau C_k+(1-\tau )C_k^T$$
• 在每一个training iteration结束时, 将$C_k$和policy preformance作为Feedback提供给LLM, 根据Feedback调整生成的函数

LESR with Discounted Return:

$u_i$将$S^C$的每一个维度映射到dense extrinsic rewards. 但是对于sparse reward settings, 将这些extrinsic rewards替换成discounted episode return ${\sum }_t{\gamma }^{t}r$.

LESR with Spectral Norm:

使用Lipschitz constant可以降低$\text{Lip}(V,S)$的上界, 改善value function的收敛性, 因此使用spectral norm去估计$\text{Lip}(V,S)$. 通过计算value function的权重$W_1,\cdots ,W_N$的spectral norm, 可以近似得出$\text{Lip}(V,S)={\prod }_{i=1}^N\Vert W_i{\Vert }_2$, 这里的$\Vert \cdot {\Vert }_2$是spectral norm.

Spectral Norm

谱范数是矩阵最大奇异值, 记为$\Vert A{\Vert }_2={\sup }_{x\ne 0}\frac{\Vert Ax{\Vert }_2}{\Vert x{\Vert }_2}={\lambda }_{\text{max}}(A)$.

几何意义: 矩阵对于输入向量的最大拉伸程度