Consistency Policy

Paper

对于diffusion而言, 可能需要多步推导, 并且中间的过程是随机的(相同的input, 随机的noise, 可能导致不同的result)

因此提出consistency policy with Q-learning(CPQL), 将多步diffusion的过程压缩成一步

Diffusion Policy for Offline RL

Offline RL

define MDP: $S,A,P,r,\gamma$

• $S$: state space
• $A$: action space
• $P(s_{t+1}|s_t,a_t)$: transition probability
• $r(s_t,a_t,s_{t+1})$: reward
• $\gamma$: discount factor

Policy Constraint for Offline Learning

假设expert dataset $D=\{(s,a,s^{\prime },r)\}$, 其action的distribution可以表示为$\mu (a|s)$. 学习一个policy $\pi$, 为了泛化OOD action, 有objective:

$$\mathcal{J}(\pi )={\mathbb{E}}_{s_t\sim D}[{\mathbb{E}}_{a_t\sim \pi (a|s_t)}[Q(s_t,a_t)]-\lambda {\mathbf{D}}_{\text{KL}}(\pi \Vert \mu )]$$

目的是让学习到的policy尽可能接近数据集的action distribution $\mu$, 减小distribution shift

Policy Improvement with Constraint Policy Search

$${\pi }^{\ast }(a|s)\propto \mu (a|s)\exp (\frac{1}{\lambda }Q(s,a))$$

Diffusion Policy

使用stochastic differential equation(SDE, 随机微分方程)进行diffusion:

$$d{a}^k=\mu (a^k,k)dk+\sigma (k)d{w}^k$$

其中:

• $\sigma (\cdot )$, $\mu (\cdot ,\cdot )$分别是是diffusion coefficients和drift coefficient
• $\{w^k{\}}_{k\in [o,K]}$表示标准布朗运动

从噪声$x^K$开始, 使用probability flow(PF) ordinary differential equation(ODE)去恢复原始数据$x^0$:

$$d{a}^k=[\mu (a^k,k)-\frac{1}{2}\sigma (k{)}^2\nabla \log p^k(a^k)]dk$$

其中未知数为score function $\nabla \log p^k(a^k)$. 那么定义一个由$\varphi$参数化的score function $s_{\varphi }(a^k,k)\approx \nabla \log p^k(a^k)$

通过设置$\mu (a^k,k)=0,\sigma (k)=\sqrt{2}$, 有PF ODE的经验估计:

$$\frac{d{a}^k}{dk}=-k{s}_{\varphi }(a^k,k)$$

难点在于计算score function, 使用guidance:

$$\nabla \log {\pi }^{\ast }(a^k|s)=\nabla \log \mu (a^k|s)+\frac{1}{\lambda }\nabla Q(s,a^k)$$

Consistency Policy with Q-Learning

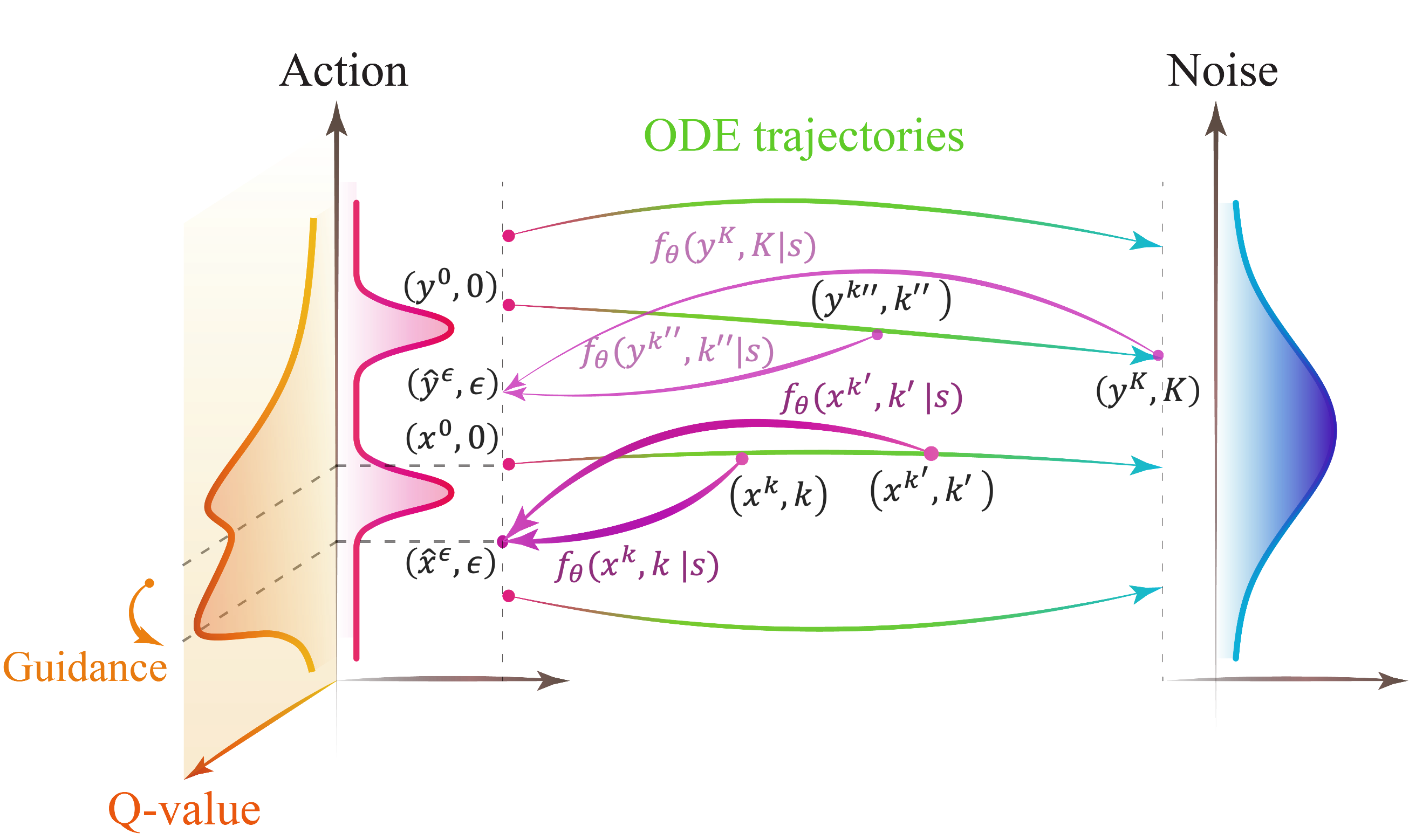
定义consistency policy:

\pi_\theta(a|s)=f_\theta(a^k,k|s)=c_{\text{skip}}(k)a^k+c_{\text{out}}(k)F_\theta(a^k,k|s)$$^policy 其中: - $a^k\sim\mathcal N(0,kI)$ - $F_\theta$是一个trainable network - $c_{\text{skip}}(\epsilon)=1$和$c_{\text{out}}(\epsilon)=0$使在$k=\epsilon$处$F_\theta$可微分 ### Training Loss for Consistency Policy $$\begin{aligned}\mathcal L(\theta,\theta^-)&=\alpha\mathcal L_{\text{RC}}(\theta,\theta^-)-\eta\mathcal L_{\text{Q}}(\theta)\\\mathcal L_{\text{RC}}(\theta,\theta^-)&=\mathbb E[d(f_\theta(a+k_{m+1}z,k_{m+1}|s),a)]\\\mathcal L_{\text{Q}}(\theta)&=\frac{1}{\mathbb E_{(s,a)\sim D}[Q(s,a)]}\mathbb E_{s\sim D,\hat a^\epsilon\sim\pi_\theta}[Q(s,\hat a^\epsilon)]\end{aligned}$$ ^loss 1. 初始化policy network $\pi_\theta$, critic network $V_\psi,Q_{v_1},Q_{v_2}$, 以及target network $\pi_{\theta^-},Q_{v_1^-},Q_{v_2^-}$ 2. 对于每一个iteration: 1. 从replay buffer中采样 2. 更新 $Q_{v_1}$([[#cpql|^CPQL]]), 或者更新 $Q_{v_2},V_\psi$([[#cpiql|^CPIQL]]) 3. 从 policy 采样 $\hat a^\epsilon_t\sim\pi_\theta(a_t|s_t)$ ([[#policy|^policy]]) 4. 更新$\pi_\theta$, 根据[[#loss|^loss]] 5. soft update: - $\theta^-=\rho\theta^-+(1-\rho)\theta$ - $v_i^-=\rho v^-_i+(1-\rho)v_i$ for $i\in\{1,2\}$ ### Policy Evaluation $$\mathcal L_Q(v_i)=\mathbb E_{(s,a,s')\sim D,\hat a^\epsilon_{t+1}\sim\pi_\theta}[\|r(s,a)+\gamma\min_{j=1,2}Q_{v_j^-}(s_{t+1},a_{t+1}^\epsilon)-Q_{v_i}(s,a)\|^2]$$^CPQL $$\begin{aligned}\mathcal L_V(\psi)&=\mathbb E_{(s,a)\sim D}[L_2^\tau(\min_{j=1,2}Q_{v_j^-}(s,a)-V_\psi(s))]\\\mathcal L_Q(v_i)&=\mathbb E_{(s,a,s')\sim D}[\|r(s,a)+\gamma V_\psi(s')-Q_{v_i}(s,a)\|_2^2]\end{aligned}$$^CPIQL 其中, $L_2^\tau(u)=|\tau-\mathbb 1(u<0)|u^2$