01-Search

前置(推荐): CS101

Search

e.g.

• problem: pathing
  • states: (x,y) location
  • action: NSEW
  • successor: update location only
  • goal test: is (x,y) = END
• problem: eat-all-dots
  • states: (x,y) dot boolean
  • action: NSEW
  • successor: update location and possibly a dot boolean
  • goal: all dots false

状态空间 states:

World State:

e.g. Pacman

• parameters
  • Agent position: 120
  • Food count: 30
  • Ghost: 12
  • Agent facing: NSEW
• World States:
  • Agent position: 120
  • food count: 2
  • Ghost: 12*12
  • Agent facing: 4
  • total: 120 * 2^30 * 12*12 * 4
• state of pathing: 120
• states for eat-all-dots: 120 * 2

针对不同的问题会有不同大小的解空间

状态空间越少越好, 状态空间越大, 搜索越多

状态空间图 State Space Graph

很少使用这种状态空间图, 因为保存的内容太多了

所以使用另外的一种算法

搜索树 Search Tree

当前状态作为一个根节点, 然后可以往不同决策行进

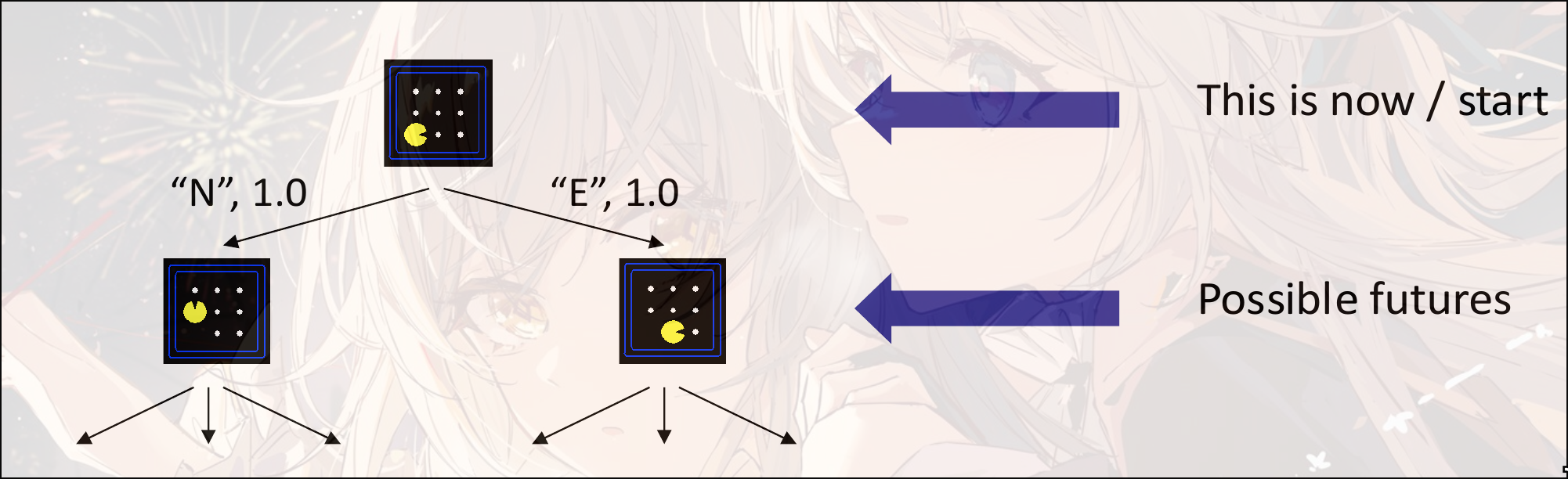
是一种”what if”树

每一个子节点都表示一种可能性(successor)

依然是无法表达出整个状态空间

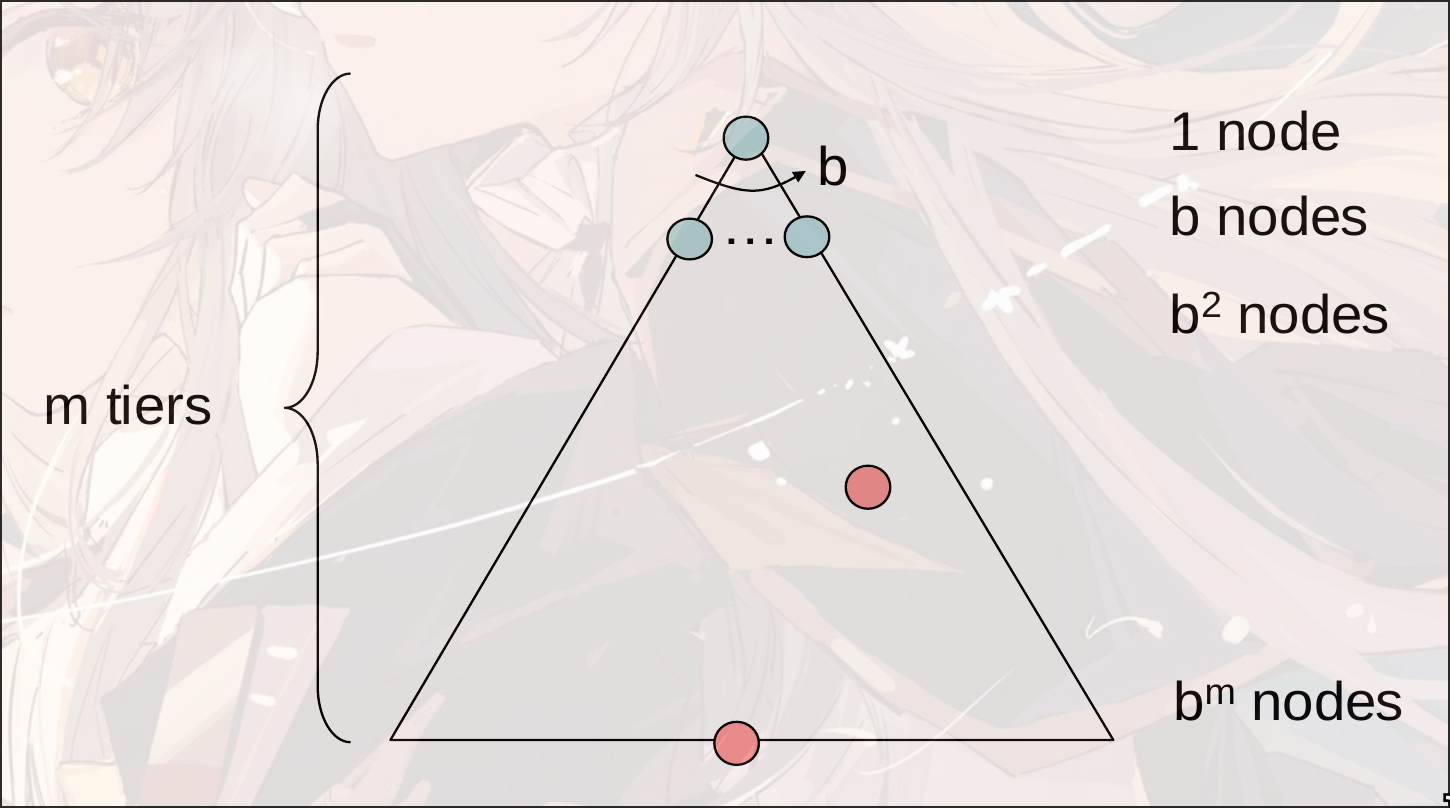
• b: branching factor: 表示一个节点可以扩展多少子节点
• m: maximum depth: 搜索可能达到的最深的路径

fringe

边缘

维护所有已扩展的路径中的叶子节点的路径(从根节点到该节点的路径)

更新: 选择一个fringe里面的叶子节点, 然后扩展到其子节点.

err

如果图上有环, 那么会导致搜索可能陷入循环, 导致没有optimal

优化: never expand a state twice. 只对某一个state搜索一次, 第二次直接停止.

不会破坏completeness, 因为所有节点还是会被访问到

different between search graph and search tree

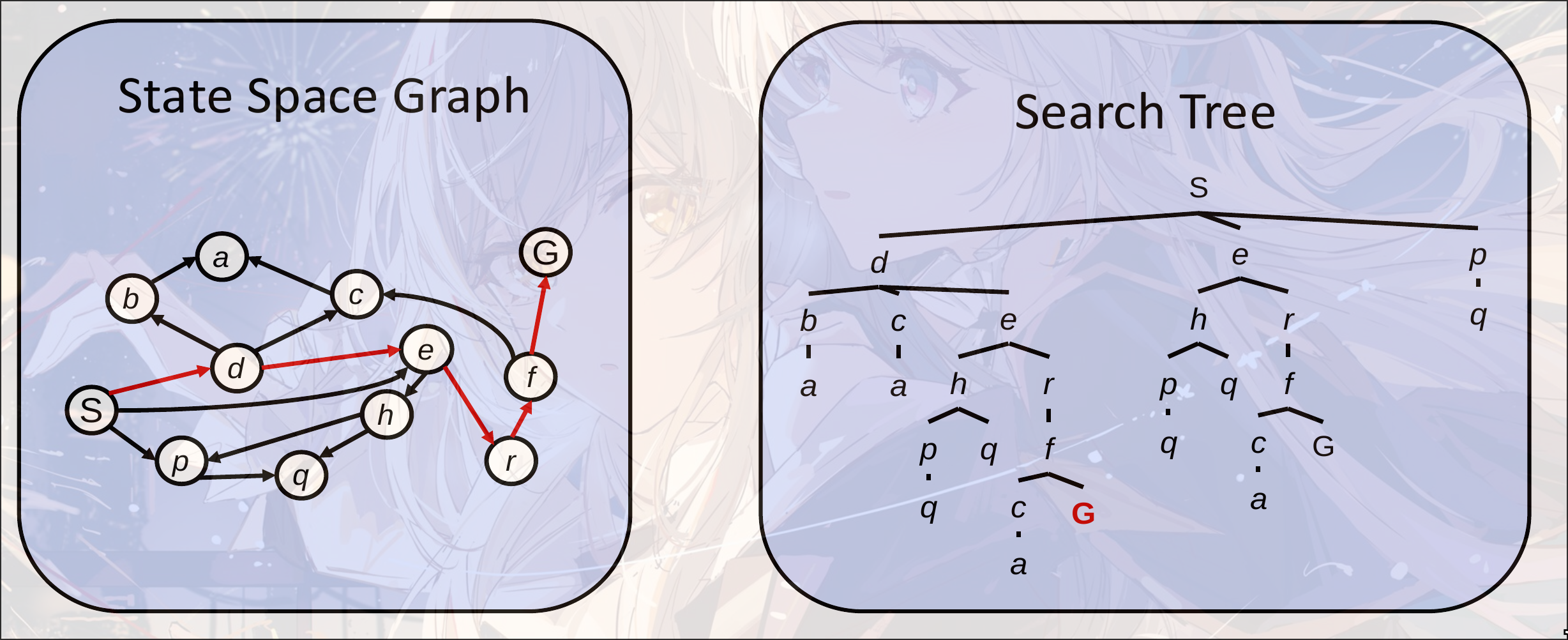
搜索

属性

• complete: 是否能找到完整的节点
• optimal: 能否找到最优解
• time complexity
• space complexity

b是branching factor: 表示多少种不同的选择

m是最大深度, 选择的次数

solutions可能在任意深度

一共有$b+b^2+\cdots +b^m=O(b^m)$

DFS

depth-first search

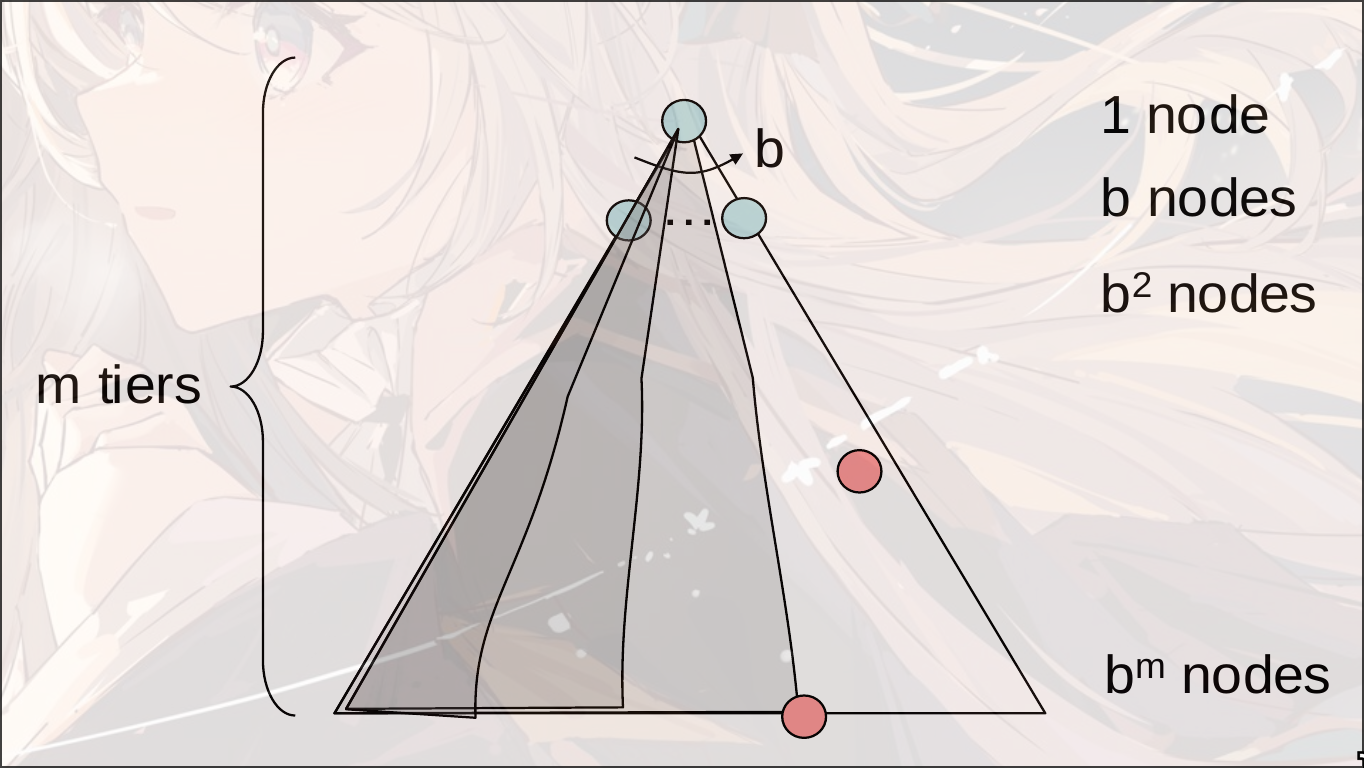
使用stack来存储

• complete: 如果深度有限那么是完整的
• optimal: 只找到了最左侧的解, 但是并没有考虑深度问题, 所以不是optimal
• time: $O(b^m)$
• space: $O(bm)$

BFS

breadth-first search

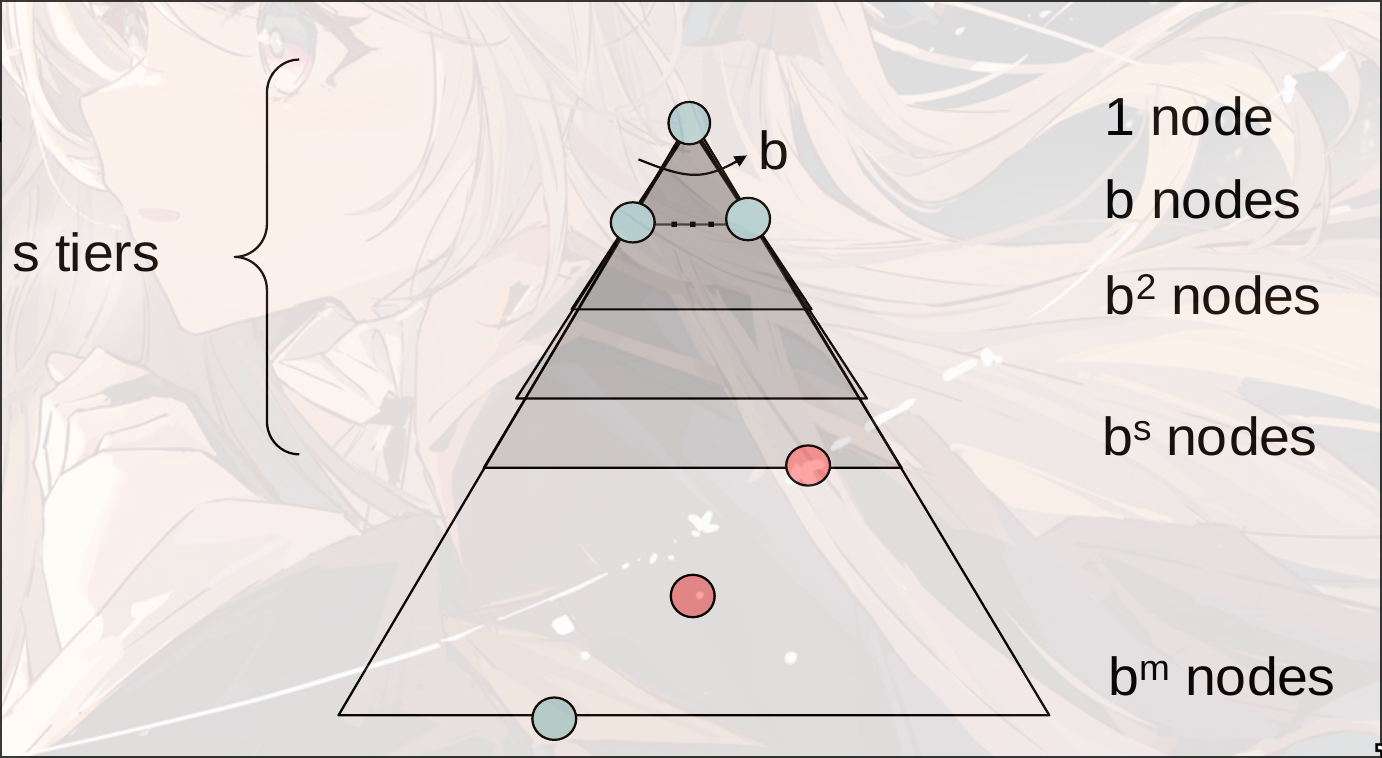
• complete: yes

• optimal: 如果每一条边的cost是1, 那么才是optimal的

• time: $O(b^s)$, 其中$s$表示搜索结果的层级

• space: $O(b^s)$

Iterative Deepening

• 限制深度为1, 进行DFS, 判断是否有解
• 如果无解, 那么限制深度为2, 进行DFS, 判断是否有解
• …

上一层的时间复杂度远远小于下一层的时间复杂度, 每一层指数增长, 上一层的搜索对下一层可以忽略不计, 因此实用性比较好

Cost-Sensitive Search

每个状态的转移具有不同的花费.

Uniform Cost Search(UCS)

strategy: 展开cost最小的node

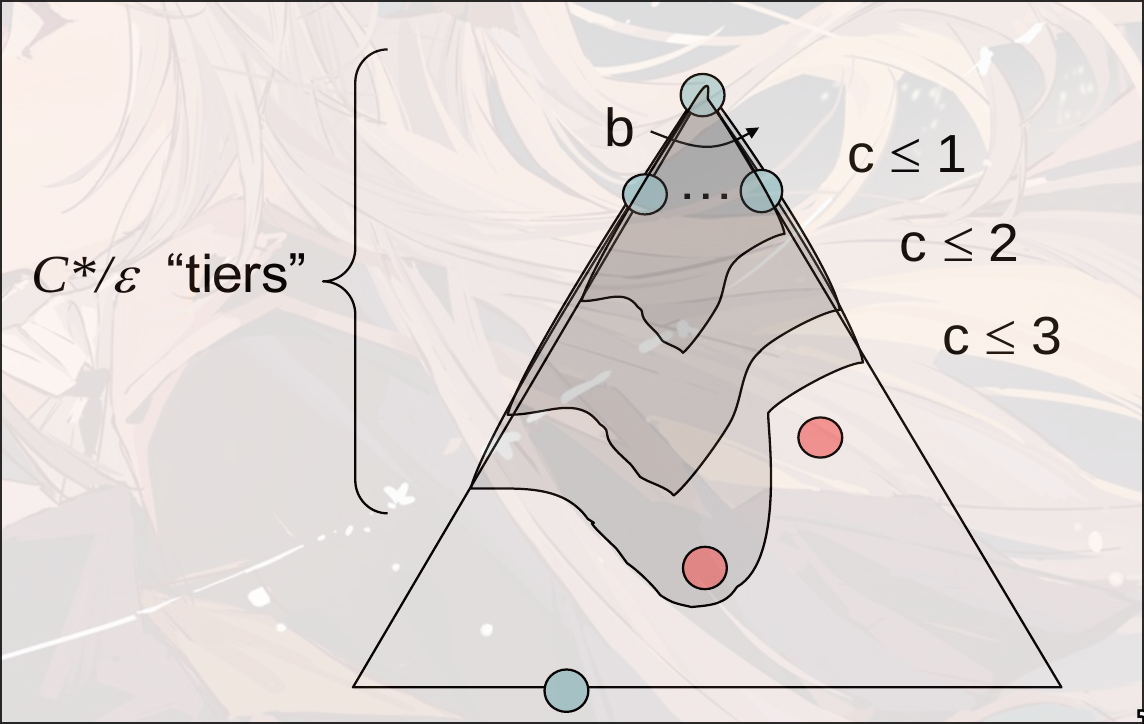
• complete:
• optimal
• time: $b^{\frac{C^{\ast }}{\epsilon }}$
• space: 存储到priority queue内部, 比较的是cumulative cost.

假设最小的花费(最优解)是$C^{\ast }$, 并且这条路上的最小花费是$\epsilon$, 那么有效路径长度大概是$\frac{C\ast }{\epsilon }$

缺点: 展开的过程中, 所有展开的距离(cost)是相同的

Model

agent对于world state的一种建模. 需要基于这个建模进行Planning和Searching

e.g. 出门是否带伞: Model: 看了天气预报 / Model: 随机带伞

Search Heuristics

目标函数: 搜索使靠近$h(goal)=0$

Greedy Search

贪心算法: 只考虑当前状态的最优解

best cases:

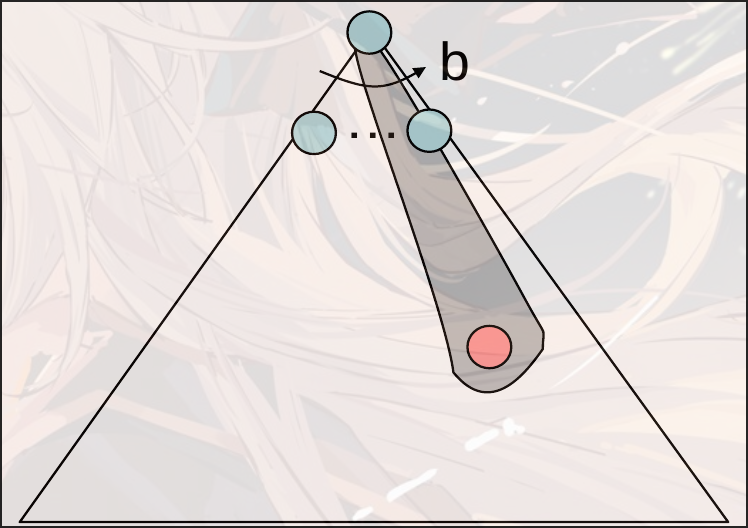
worst cases:

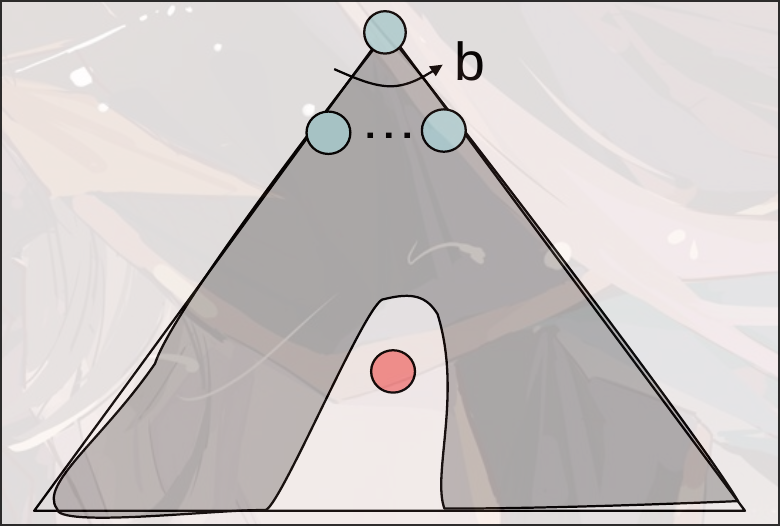
A* Search

uniform-cost search: backward cost 路径的花费: $g(n)$

greedy search: forward cost 未来估计价值: $h(n)$

A* search: $f(n)=g(n)+h(n)$

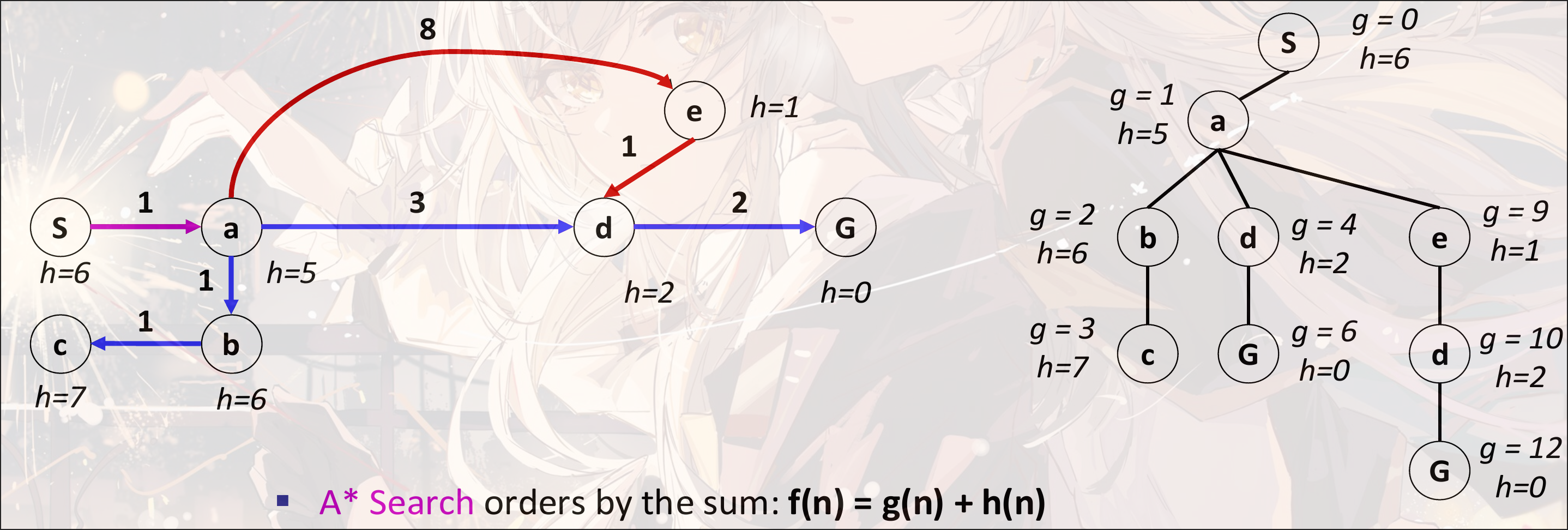
• complete: 需要让$h(n)$是admissible: $0<h(n)<h^{\ast }(n)$其中$h^{\ast }(n)$是真实距离

• optimal:

  假设:

  • 任意节点$n$, 最优解$A$, 次优解$B$

  Claim:

  • A will exit fringe before B

    A比B先弹出fringe, 表示A会先进行is_goal的测试

  Proof:

  • $$textadmissive\Rightarrow h(n)\le h^{\ast }(n)=g(A)-g(n)$$ $$h(A)=0\Rightarrow f(A)=g(A)\Rightarrow h(n)\le f(A)-g(n)$$ $$\Rightarrow h(n)+g(n)\le f(A)\Rightarrow f(n)\le f(A)$$ 因此, 节点$n$一定在节点$A$之前找到
  • $$\text{A is optimal and B is suboptimal}\Rightarrow g(A)<g(B)$$ $$\text{A, B are goal}\Rightarrow h(A)=h(B)=0\Rightarrow f(A)<f(B)$$ $$\Rightarrow f(n)\le f(A)<f(B)$$ $$\Rightarrow \text{n比B先expand}$$
  • A的所有祖先节点都比B先expand
  • A比B先expand

  所以是optimal的

heuristics越接近真实cost, 搜索代价就越小

admissible

$0<h(n)<h^{\ast }(n)$其中$h^{\ast }(n)$是真实距离

consistency

$h(A)-h(C)\le h^{\ast }(A-C)$

其中$h^{\ast }(A-C)$表示A到C的实际距离

consistency可以推出admissible

$$h(C)=h(C)-h(goal)\le h^{\ast }(C-goal)=h^{\ast }(C)$$