03-AdversarialSearch

前置要求: 01-Search

Adversarial Search

Game Type:

• 是否确定(只能选择一个或几个行为之一) Deterministic or stochastic
• 玩家个数
• 是否零和博弈 zero sum
• 是否观测到当前状态的所有信息 Perfect Infomation

目的是找到一个policy(strategy), 能够给定任意的state $S$, 找到一个行为action $A$

Search

Single-Agent Tree

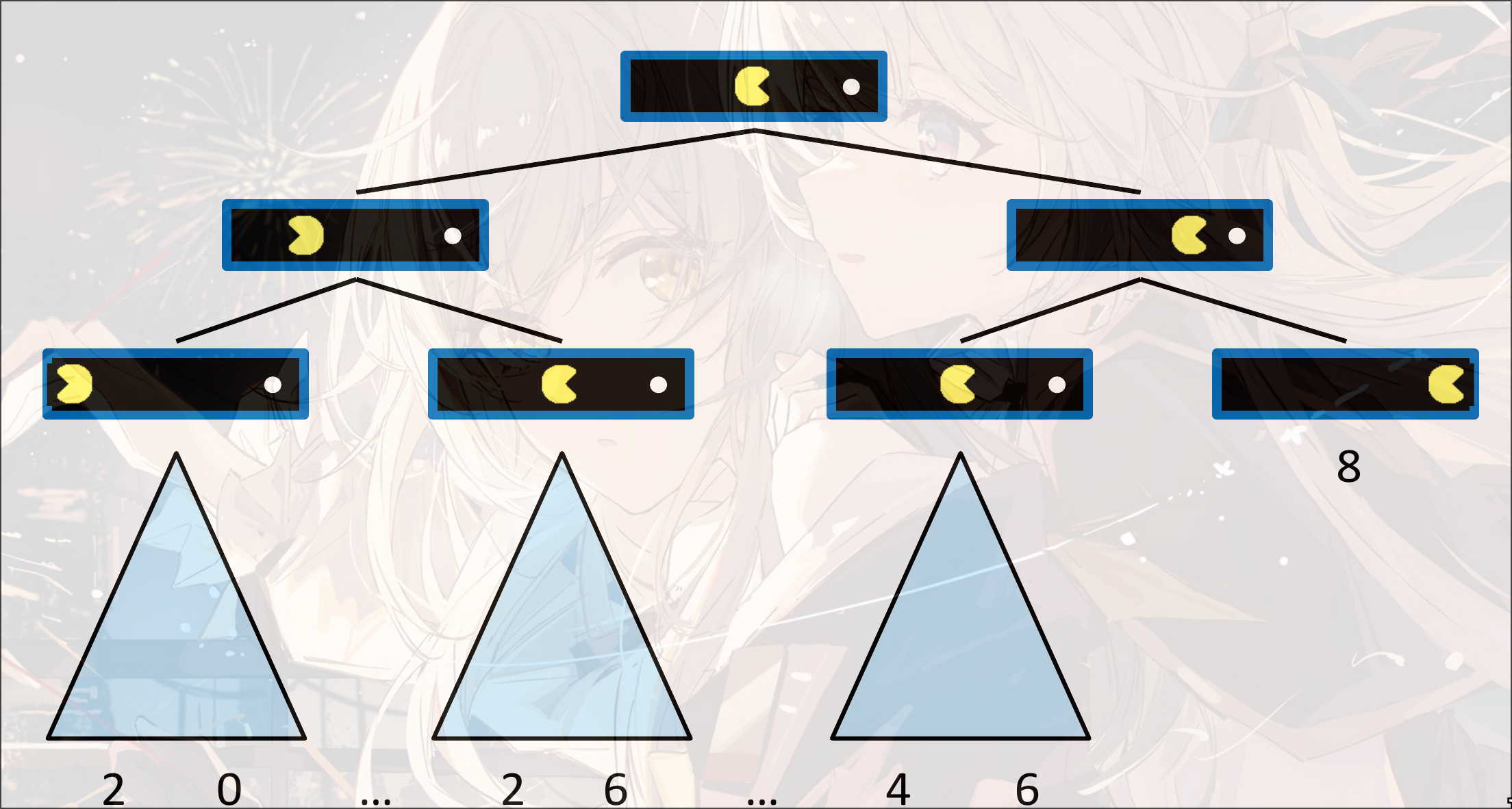
Minmax Search

对抗: 红色状态是敌人的agent, 要让红色状态的state value越小越好, 蓝色状态的state value越大越好

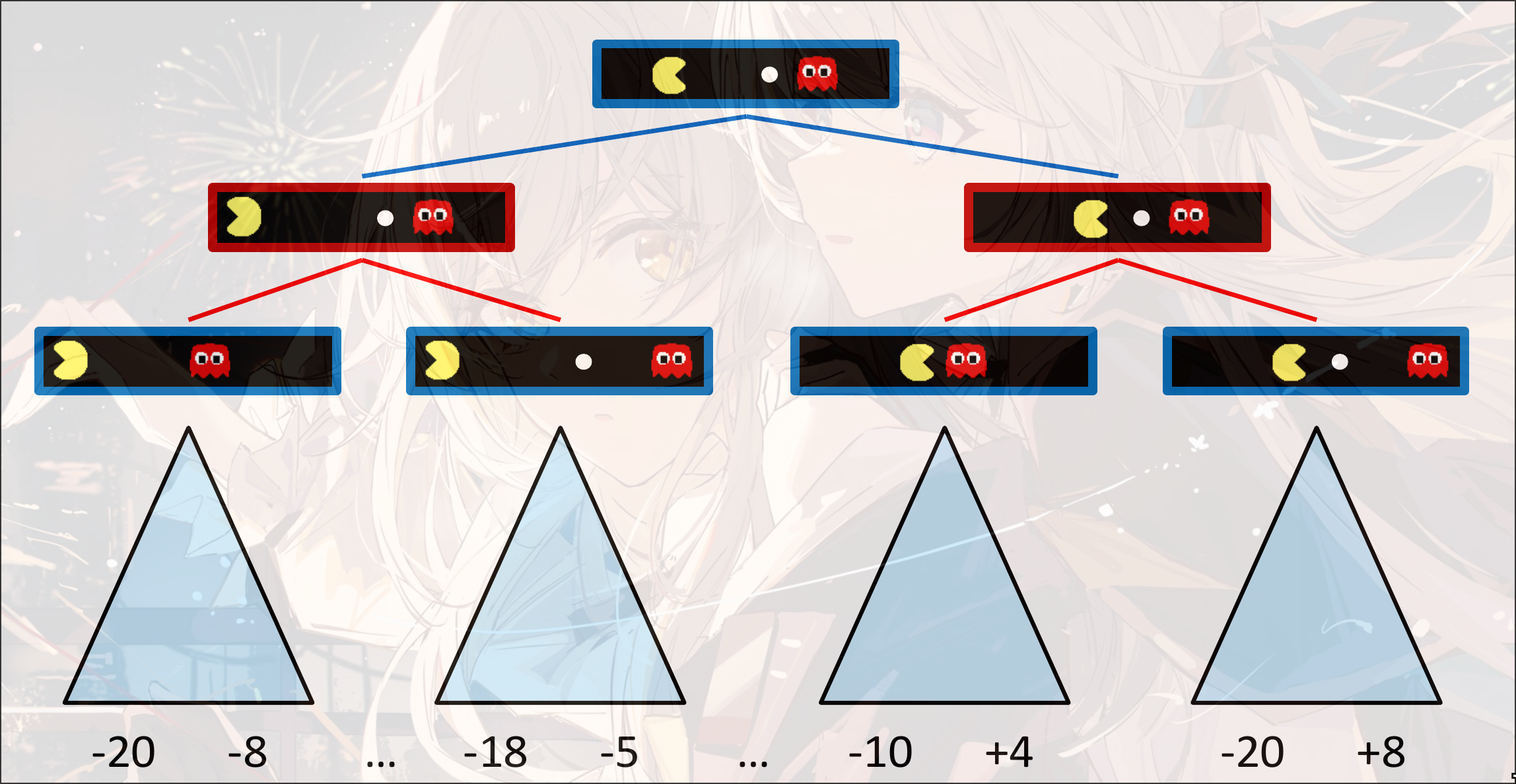
• 如果是终止状态, 直接返回终止状态的value
• 如果是max, 寻找最大化的state value: max(v, value(successor))
• 如果是min, 寻找最小化的state value: min(v, value(successor))

是类似穷举的DFS

时间复杂度: $O(b^m)$

空间复杂度: $O(bm)$

$b$是state, $m$是步数

Improve

depth-limited search

在有限深度下搜索

Evaluation Function: 对非终止节点的state value的估计, 根据不同的特征进行判断

理想方程: 真实的minmax search的state value

Monte Carlo Tree Search

对树进行采样, 控制采样的深度和次数, 对采样的结果进行统计, 可以得出原始的树的state value和distribution

Game Tree Pruning

Minmax Pruning

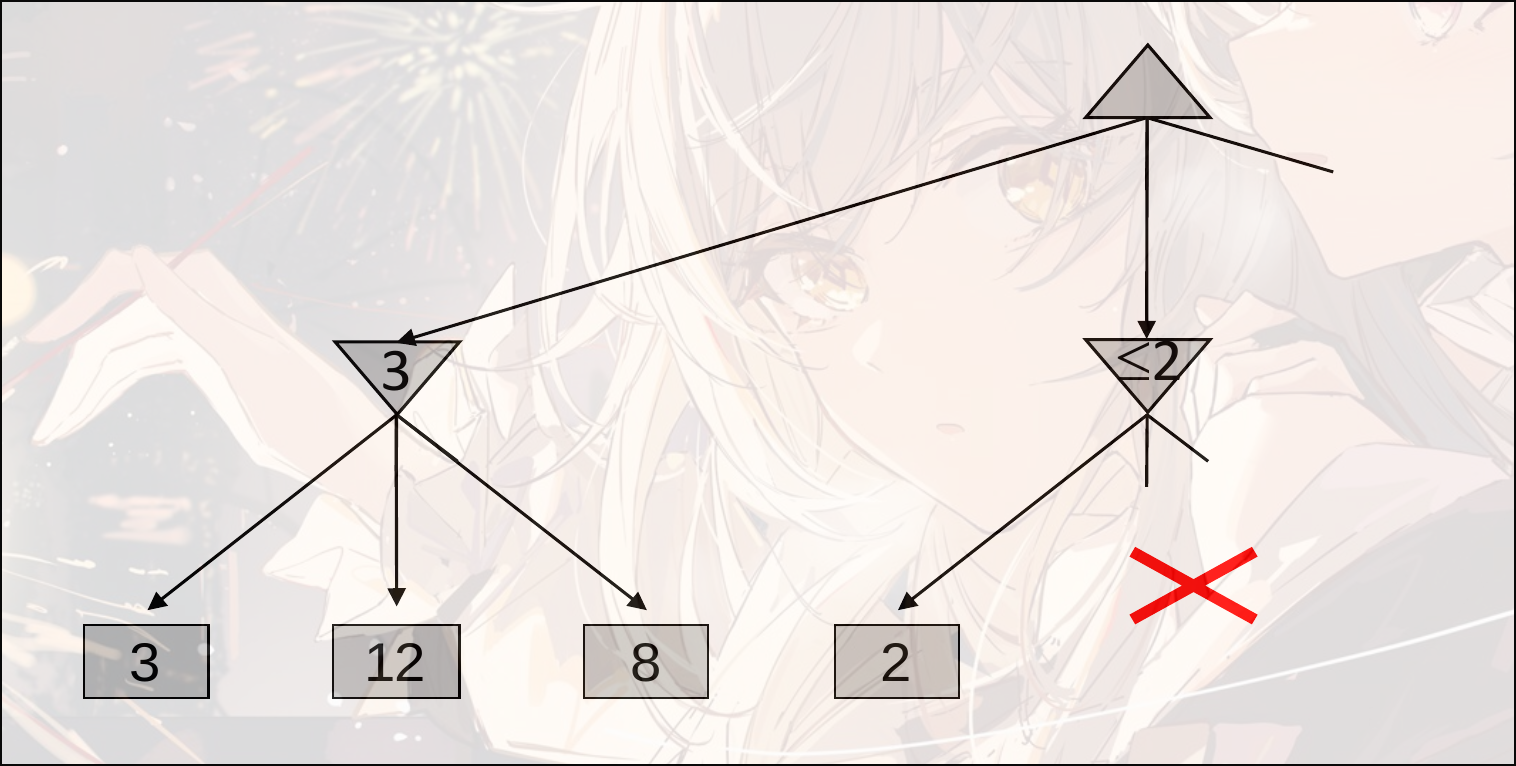
第一步找到了3, 第二步中, 找到了一个2, 那么第二步的min的state value一定是一个小于2的值, 那么可以直接舍去这一个选择(要选择max的state value)

Alpha-Beta Pruning

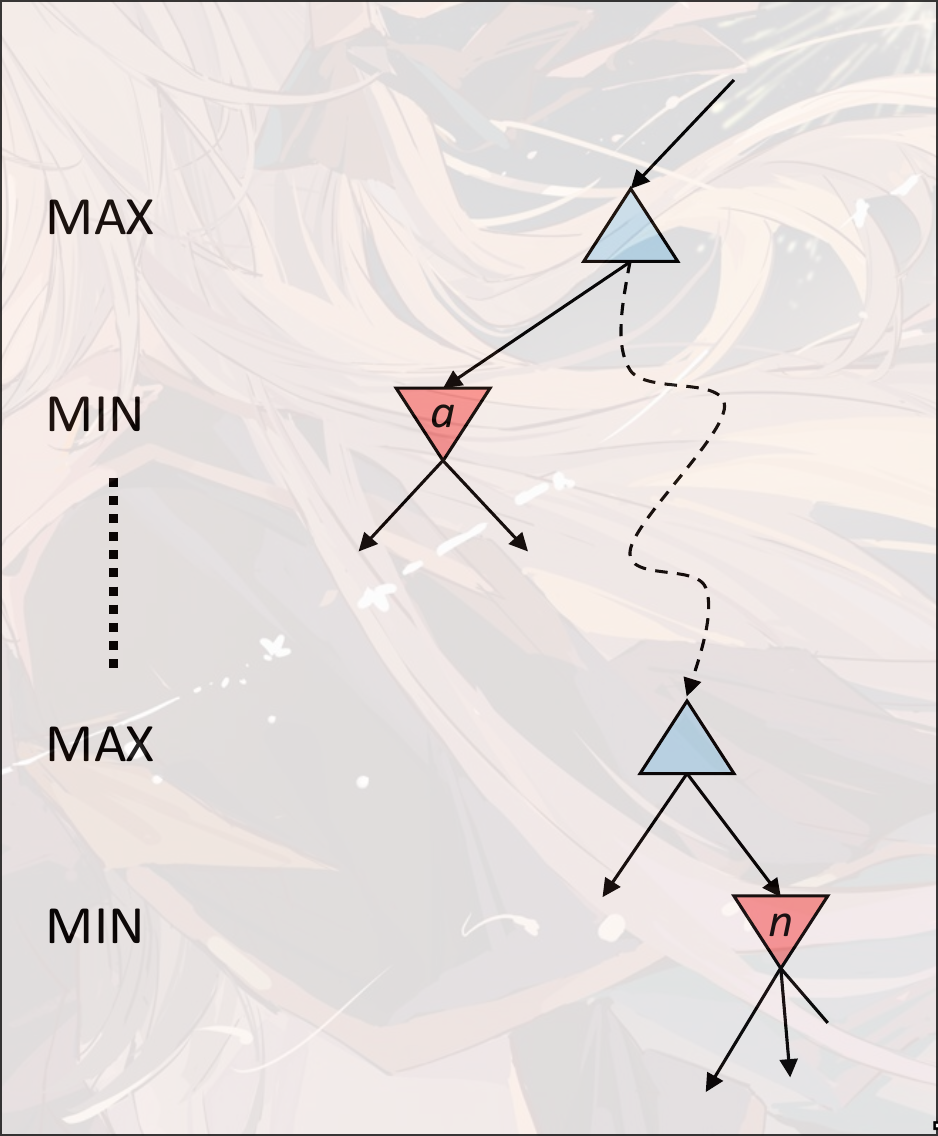
• 假设现在对节点n计算state value
• 展开n的节点的子节点. 因为是取最小, 那么展开n的子节点的过程中, n的state value一定是递减的
• 假设a是MIN层中最大的节点
• n的state value一旦小于a的state value, 那么在向上传递的过程中, 在与a同层的位置一定会选择更大的a而不是n的state value
• 所以可以直接舍去n节点的后续计算

Implementation:

• 初始化$\alpha$是MAX的最优选项, $\beta$是MIN的最优选项
• max value:
  • 初始化$v=-\infty$
  • 更新每一个successor
    • v = max(v, value(successor))
    • 如果$v\le \beta$, 那么直接不计算(剪枝)
    • 更新$\alpha =\max (\alpha ,v)$
• min value:
  • 初始化$v=+\infty$
  • 更新每一个successor:
    • v=min(v, value(successor))
    • 如果$v\ge \alpha$, 剪枝
    • 更新$\beta =\min (\beta ,v)$