前置: 04-PropositionalLogic 05-BayesNetwork
Bayes Net: Exact Inference
Variable Elimination
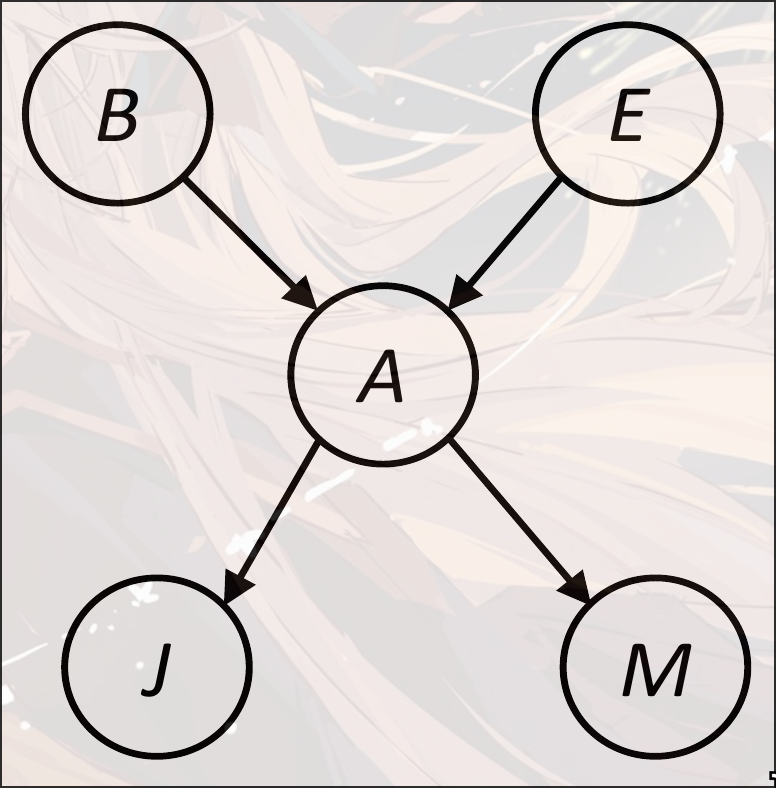
考虑
可以将原本16乘法7加法转换成2乘法3加法
于是考虑隐变量的因子消除方法:
但是有一个问题. 在计算的时候, 不是一个正常的实数, 而是一系列与有关的值. 所以在计算的时候, 需要把他们当成一个多元的变量, 称作factor
operation
-
Join Factors
给定多个CPT, 将多个CPT整合成一个CPT
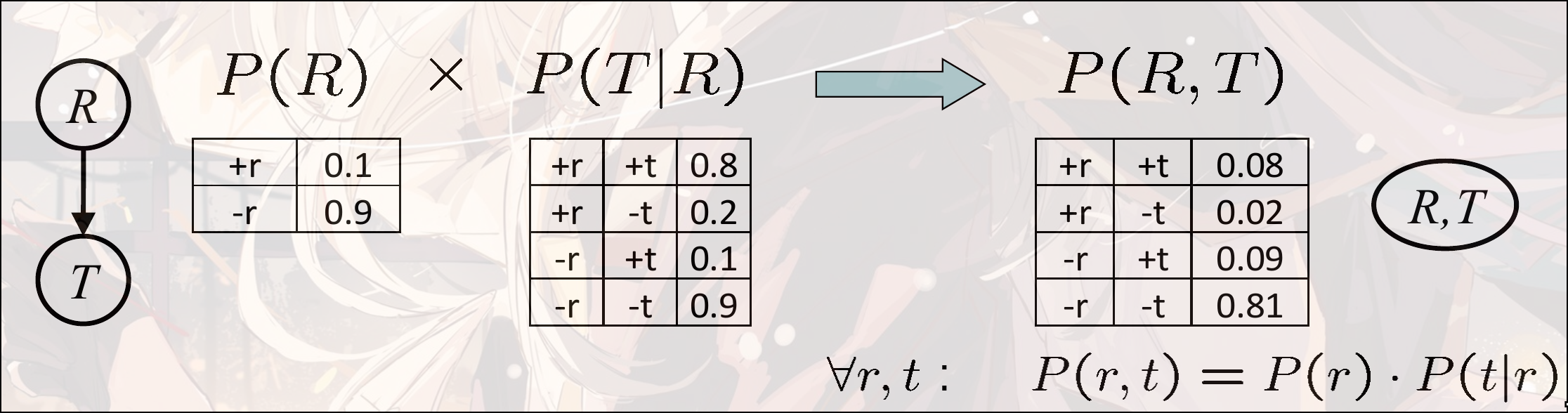
-
Variable Elimination
将隐变量求和, 消除
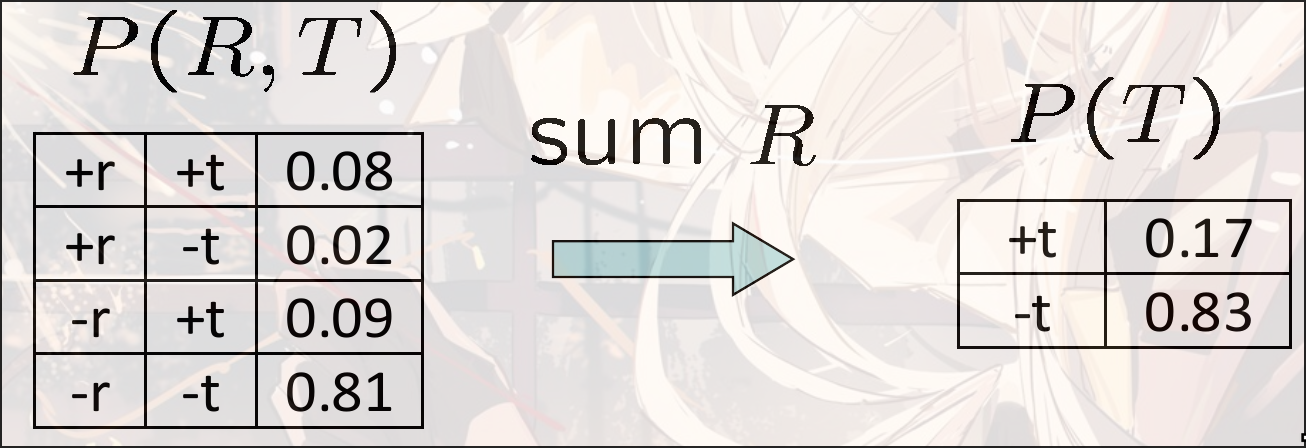
假设求
- 从local CPT开始
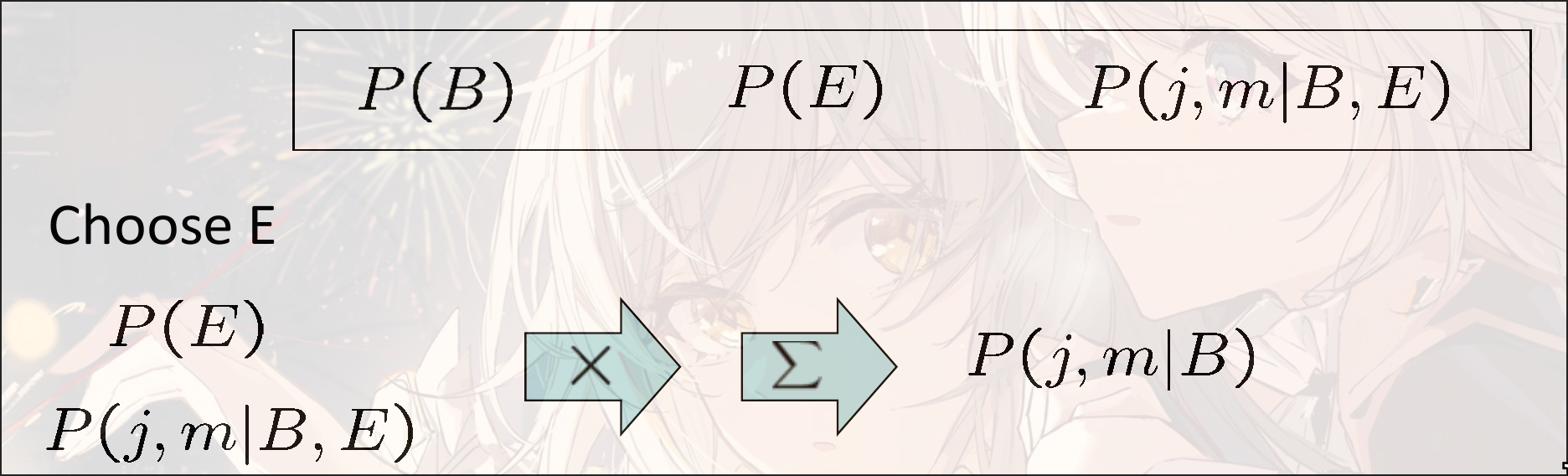
- 选择一个隐变量
- 将所有提到的factor进行join
- 对进行求和(sum elimination)
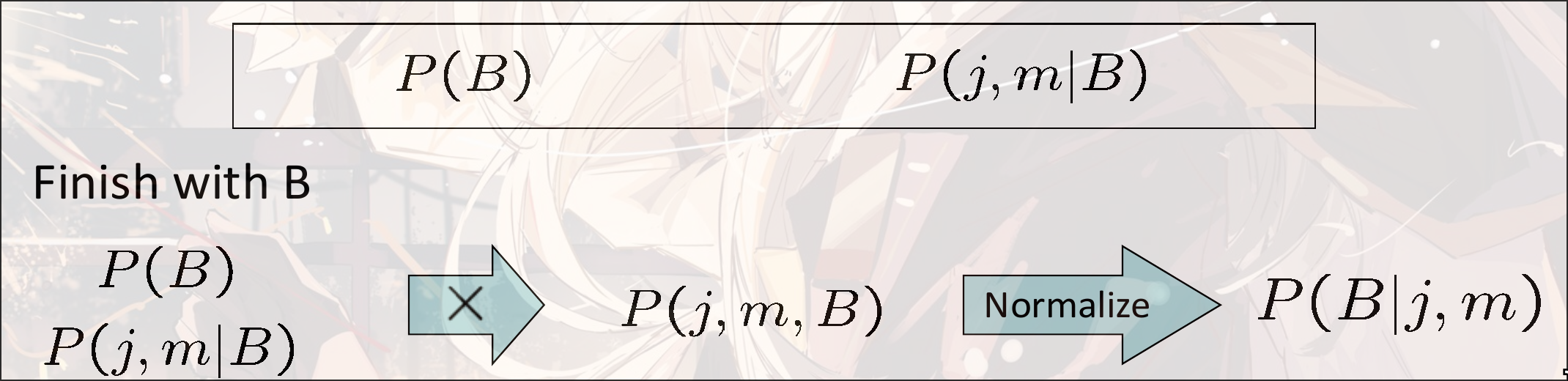
- 重复, 直到只剩下和
e.g.

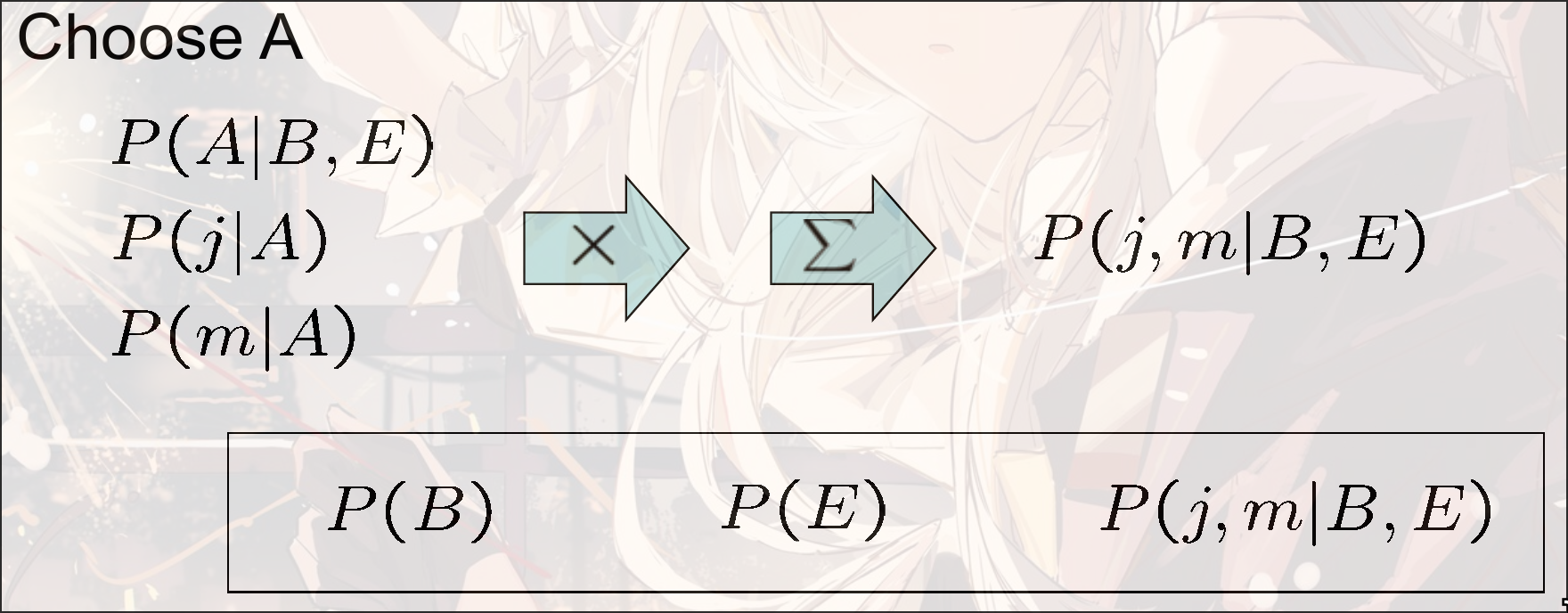
Ordering Matter
graph TB Z-->A Z-->B Z-->C Z-->D
假设我们需要计算
那么所有其他的变量都是hidden variable
-
如果消除顺序为
P(D)=\alpha\sum_{a,b,c,z}P(z)P(D|z)P(A|z)P(B|z)P(C|z)$$ $$=\alpha\sum_{z}P(z)P(D|z)\sum_aP(A|z)\sum_bP(B|z)\sum_cP(C|z)CBAZ -
如果消除顺序为
ZABC
消除顺序不同则参数量不同
不存在一种最小的复杂度对于一个Bayes Network Variable Elimination. 这个和图的结构有关
Message Passing and General Graphs
graph LR A---B C---B B---D D---E D---F
对于poly-tree的网络, 可以看作图上的信息的传播. 将算好的概率传播
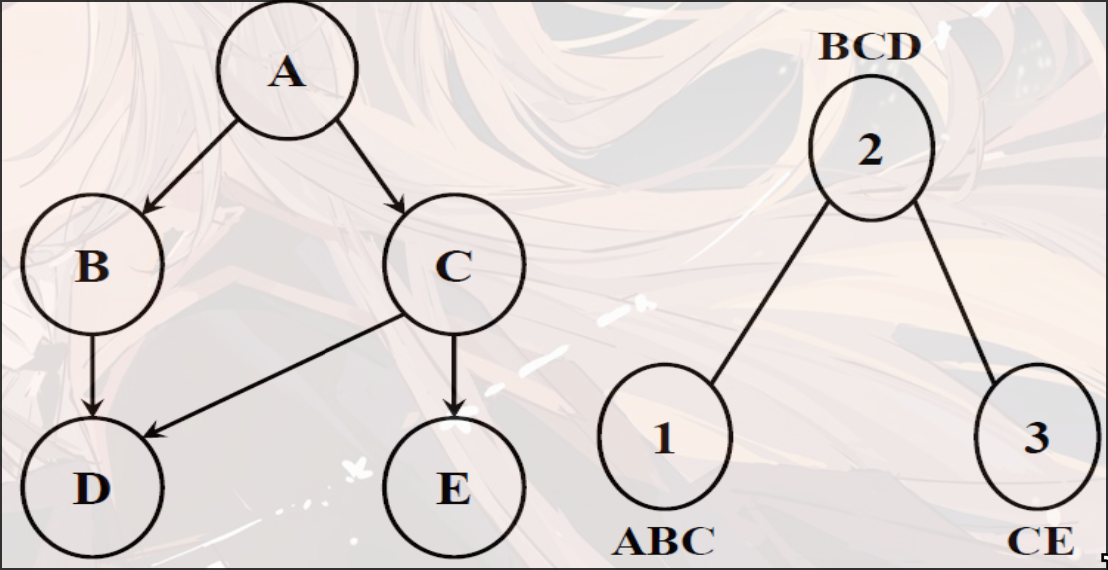
分团之后, 两个团的连接点必须同时出现在两个团中. 如 cluster1: , cluster2: , 相连的两个点是和, 那么这两个点必须在这两个cluster中同时出现
Bayes Net: Approximate Inference
Sampling from given distribution
-
step1: 从一个
[0, 1)的uniform distribution采样一个u有多重方式实现, 如:
import random u = random.random() -
step2: 从采样的概率中获取到变量
如:
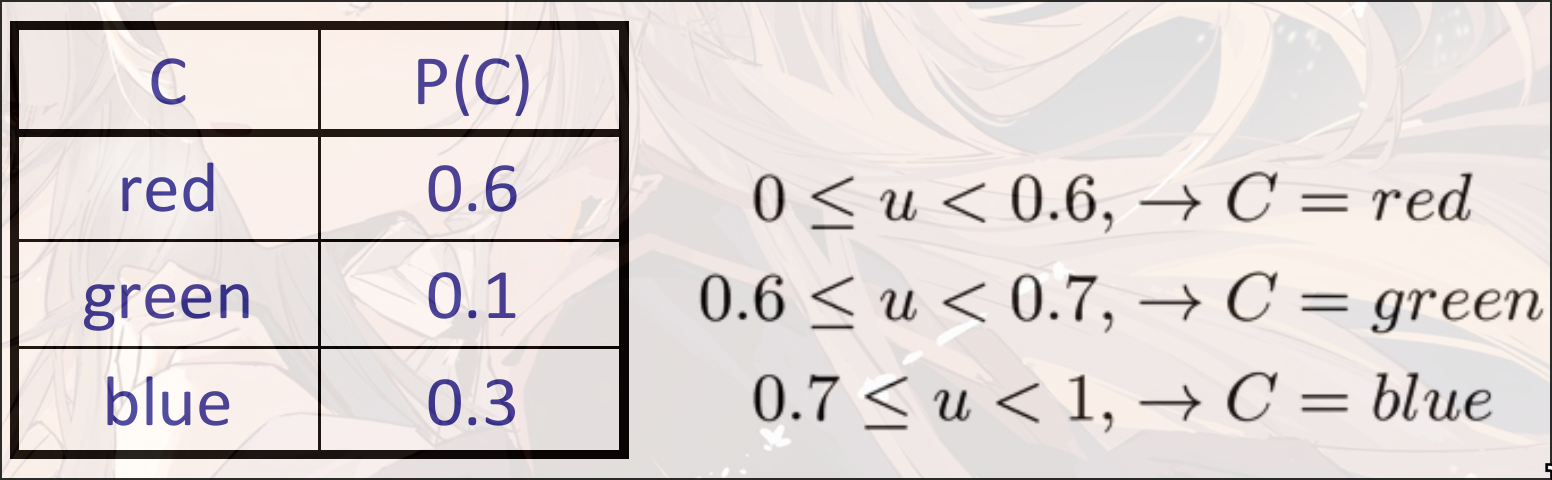
Prior Sampling
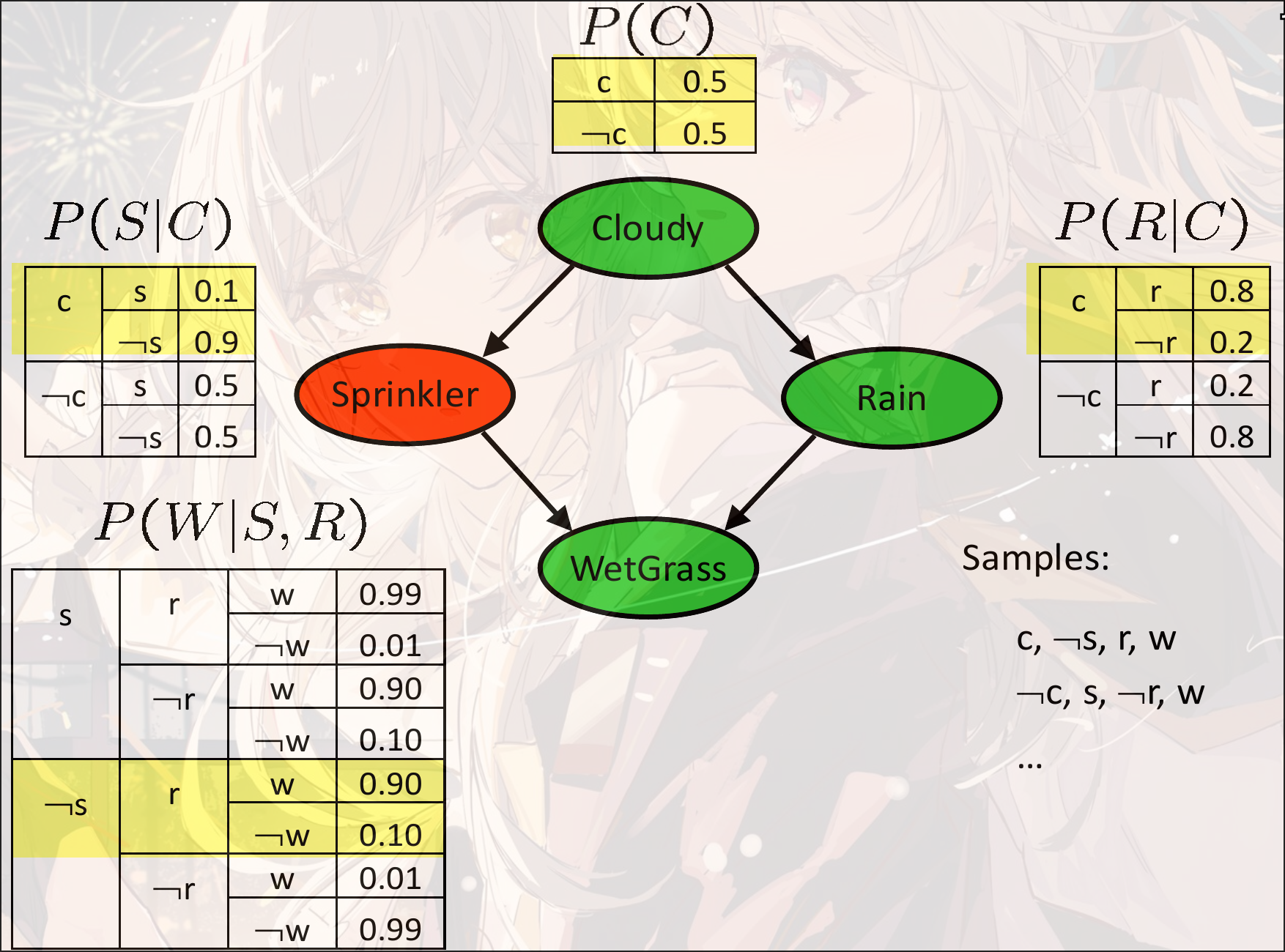
先根据的概率采样:
然后已知的情况下采样 ,
然后在已知的情况下采样:
最终得到
重复多次
采样的顺序最好为Bayes Network的拓扑结构(有了condition才能更好算出当前的结果)

采样多次之后, 假设我们有
如果要计算, 那么有, 则
Tip
算法推导:
- 根据真实概率采样
_{Prior Sample}(x_1,\cdots,x_n)=\prod_iP(x_i|\text{Parent}(x_i))=P(x_1,\cdots,x_n)$$
- 采样得到的概率有
hat P(x_1,\cdots,x_n)=\frac{N_{Prior Sample}(x_1,\cdots,x_n)}{N}$$
- 则当采样次数时:
lim_{N\to\infty}\hat P(x_1,\cdots,x_n)=\lim_{N\to\infty}\frac{N_{Prior Sample}(x_1,\cdots,x_n)}{N}$$
Rejection Sample
假设我们需要计算, 即需要已知的概率, 那么我们直接不需要采样(记录)出现或者的情况

有问题:
假设condition本身就是很小的概率, 那么我们的概率可能很小或者极大.
如:
graph LR a[Shape]-->b[Color]
假设, 那么本身出现blue的概率很小, 那么如果采样Shape, 很容易出现极端情况
Likelihood Sample
为了解决Rejection Sample的问题, 我们首先固定已知的变量, 在这种情况下进行采样, 而不是直接采样然后拒绝
将所有采样的Evidence的条件概率相乘作为权重
然后在计算概率的时候, 我们并不是使用出现的个数, 而是使用采样对应的权重进行计算
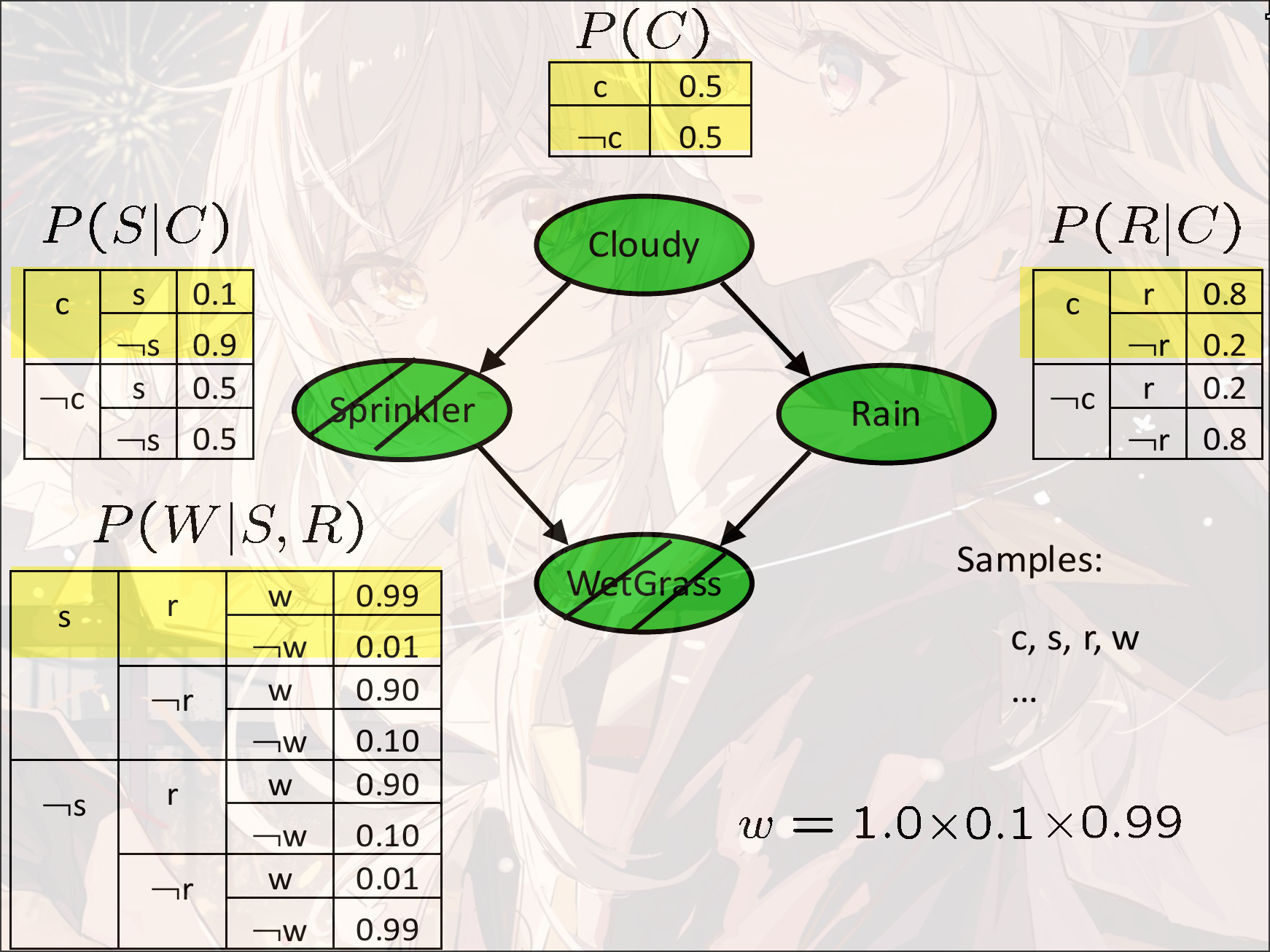


那么有
然后归一化
Tip
正确性推导
Importance Sample
使用Likelihood Sample的优化, 改变weight的计算
假设很小, 那么很难采样. 我们可以自己设计一个分布, 然后根据进行采样, 最终使用作为权重
选取对算法的影响很大. 最好的应该是
Gibbs Sample
原先的采样是, 现在我们认为采样的时候与其他所有的变量相关, 即
但是注意有Markov Blanket阻断其他变量的信息流通, 那么我们其实只需要关注:
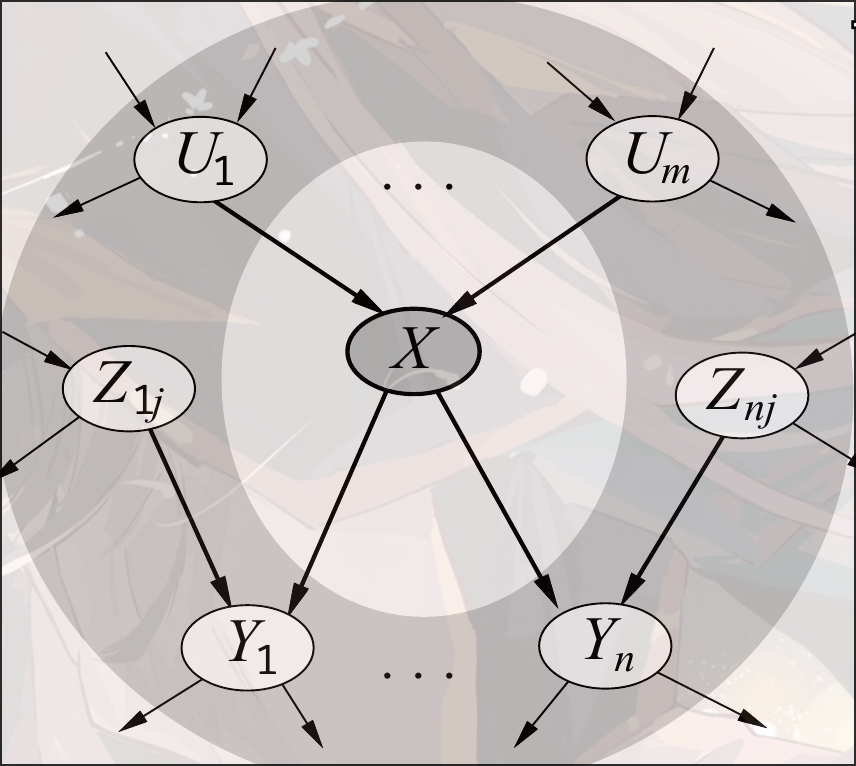
Markov Chain Monte Carlo(MCMC)
Markov Chain是一个条件假设: 每一个状态只依赖于前一个状态而不是全局状态
Monte Carlo: 采样算法
Metropolis-Hastings
在给定分布下进行采样
- 是一种易于采样的分布
有概率接受这个采样, 接受概率为