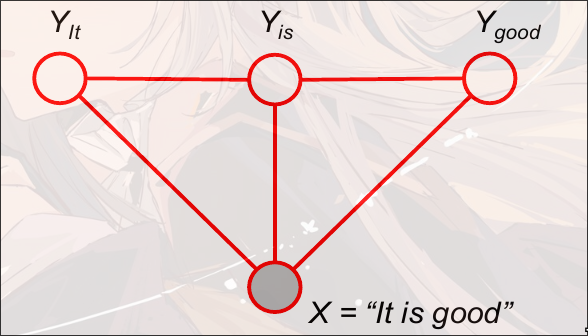
前置要求: 04-PropositionalLogic
Bayes Network
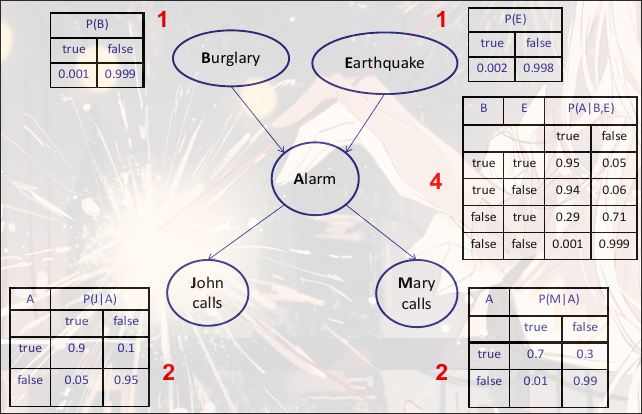
CPT: Conditional Probability Table
独立:
条件独立: 给定某个条件下, 两个事件相互独立
写作
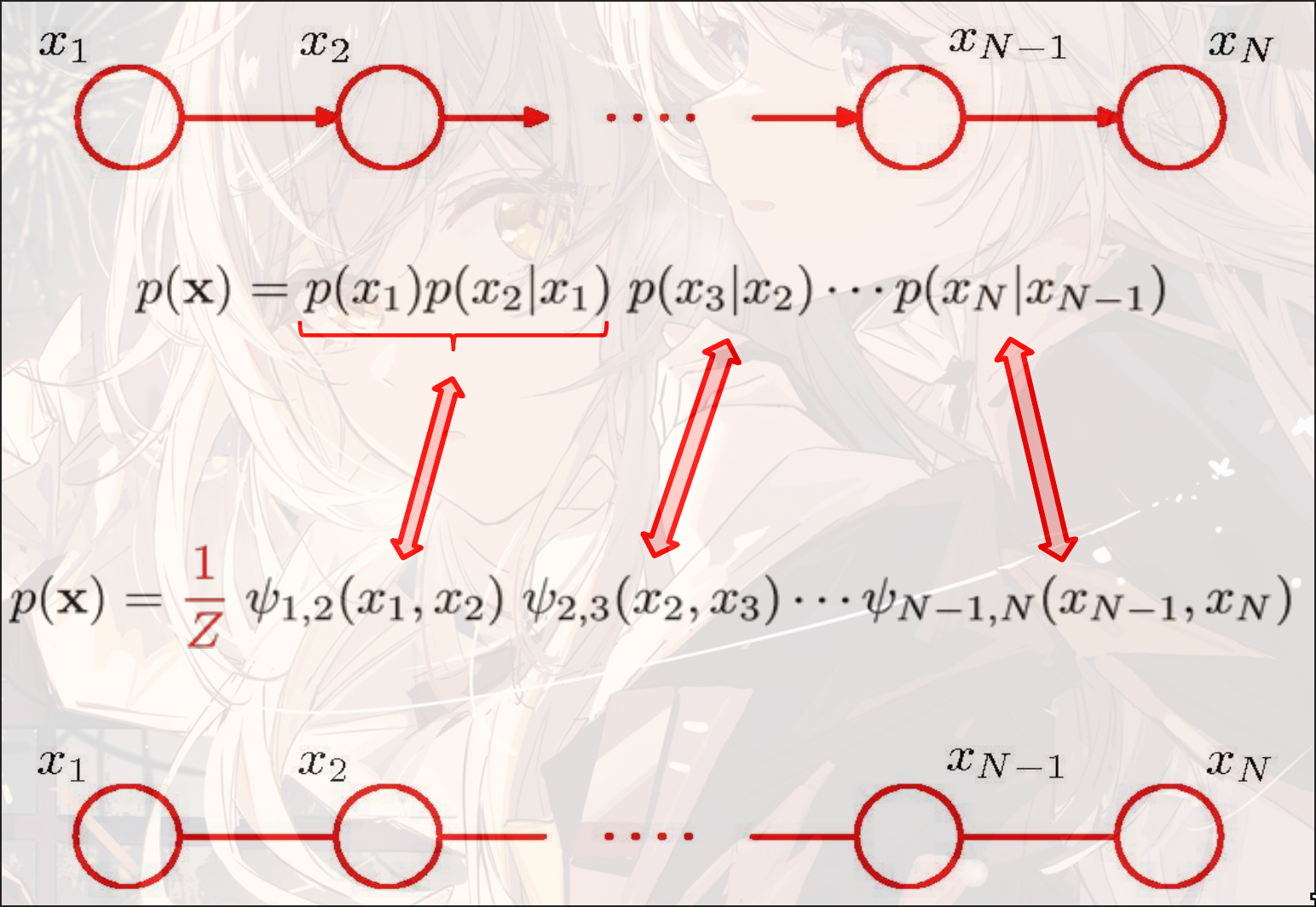
链式法则chain rule:
可以在使用链式法则的时候使用条件独立化简条件:
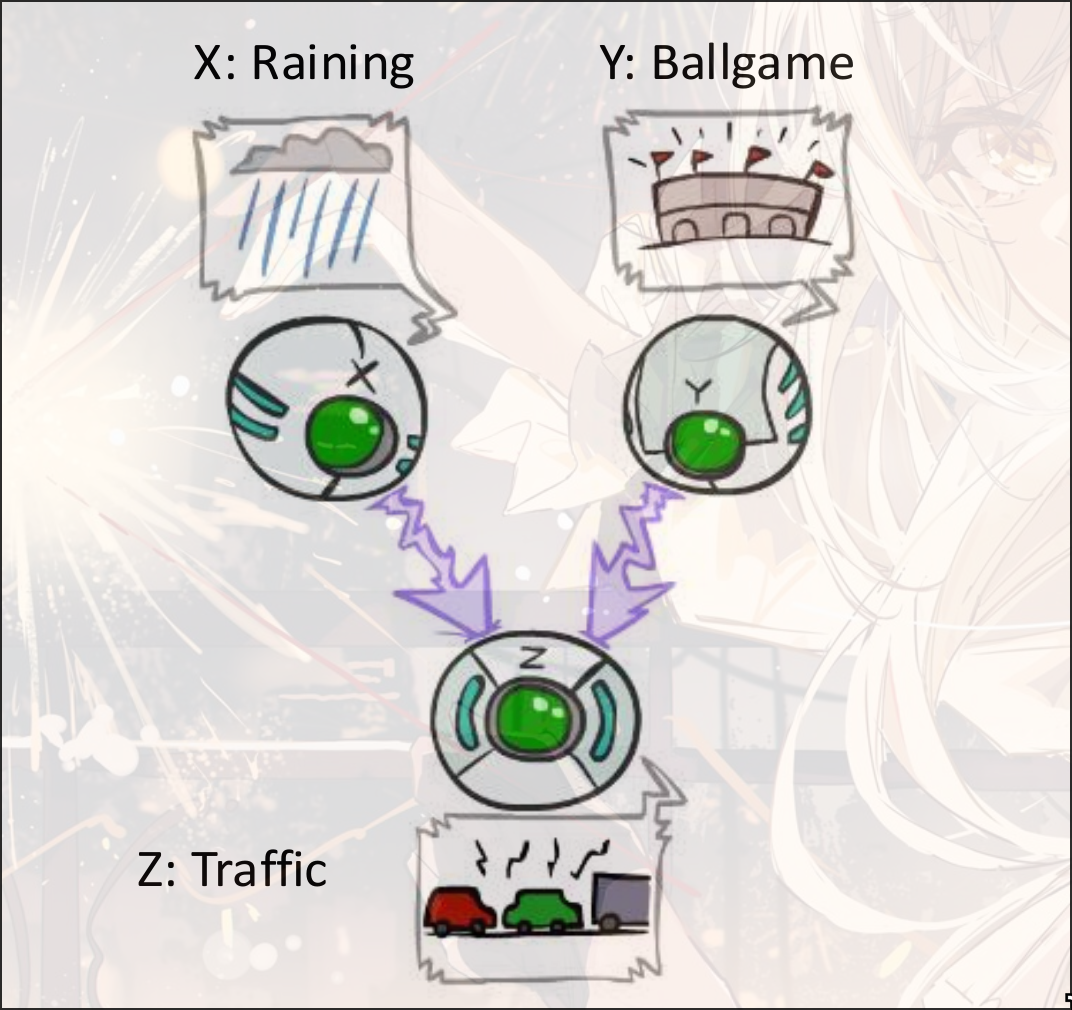
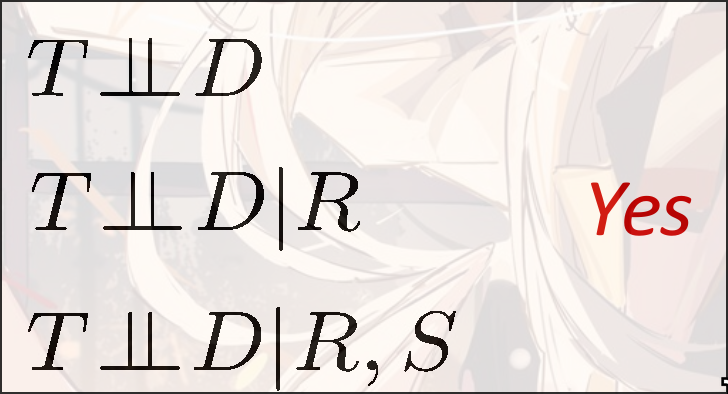
e.g.: Traffic, Umbrella, Rain
对于某一个子节点:
- 假设父节点的domain为
- 假设该节点的domain为
- 每一行之和是1
- 那么该节点的复杂度(参数量)是
- 的原因是行之和为1
对于一个Bayesian Network:
- 个变量
- 最大的domain是
- 最大的父节点数量是
全联合概率密度分布是
Bayes Net的空间是
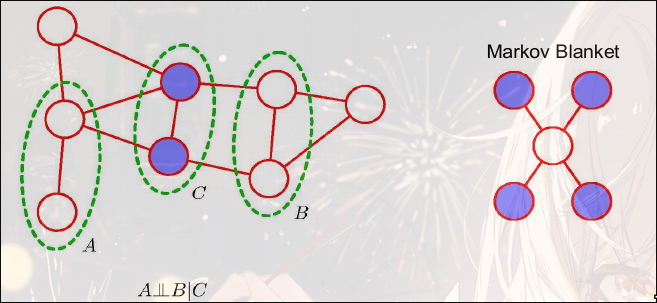
Markov Blanket
给定父节点, 子节点, 子节点的父节点, 然后该节点与其他所有节点条件独立
-
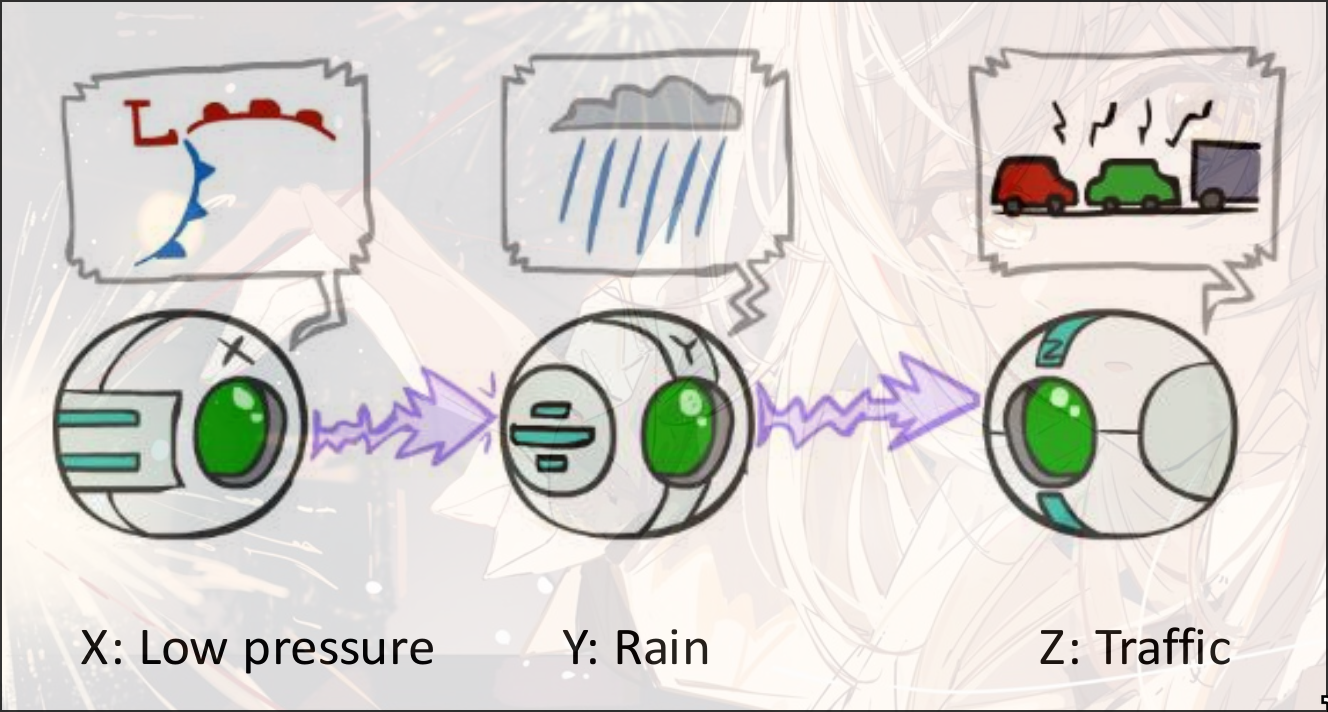
causal chain
Global semantic:
给定, 有
-
Global semantic:
给定, 有
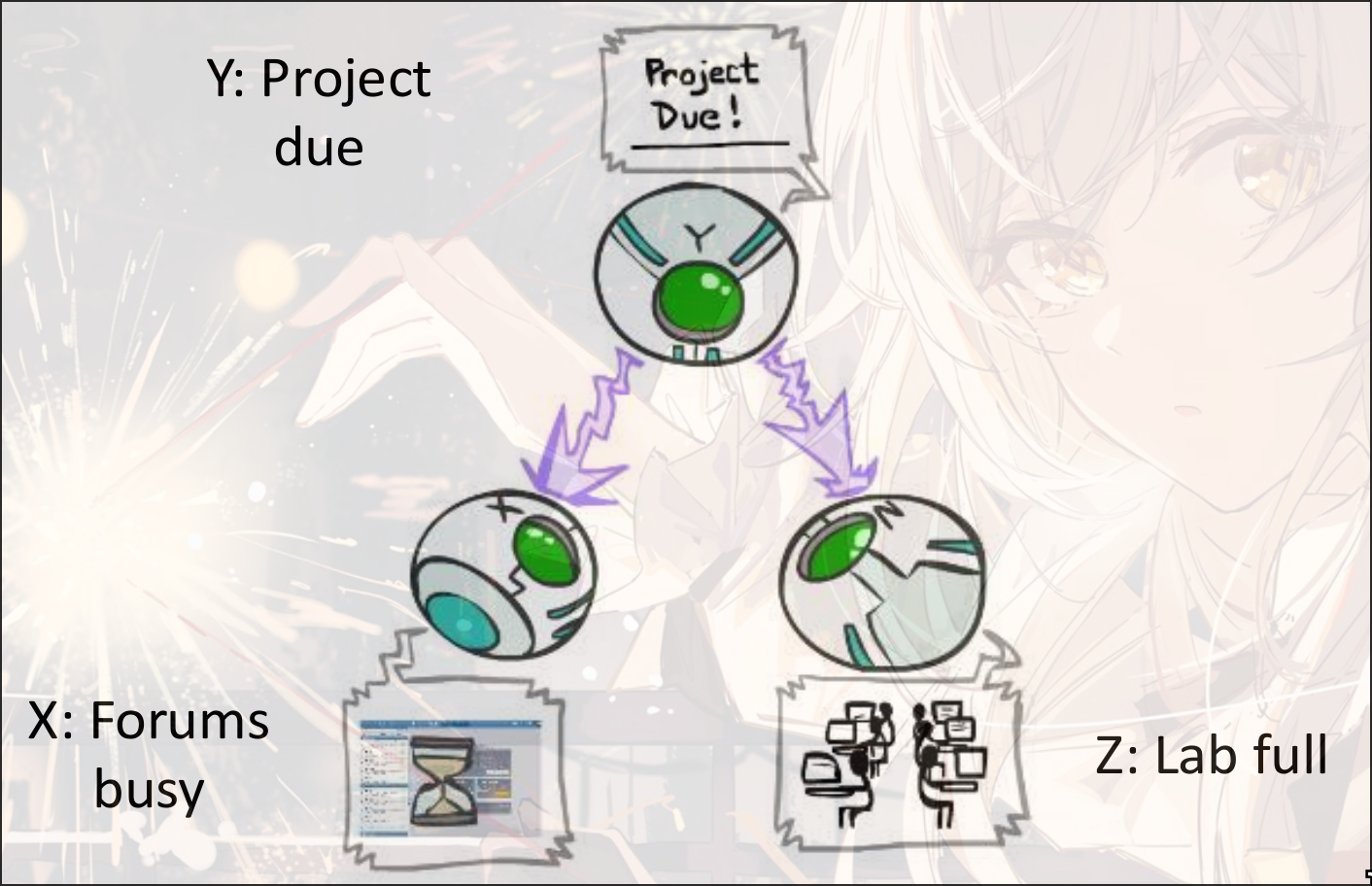
-
若不给定, 那么
给定, 有与不独立
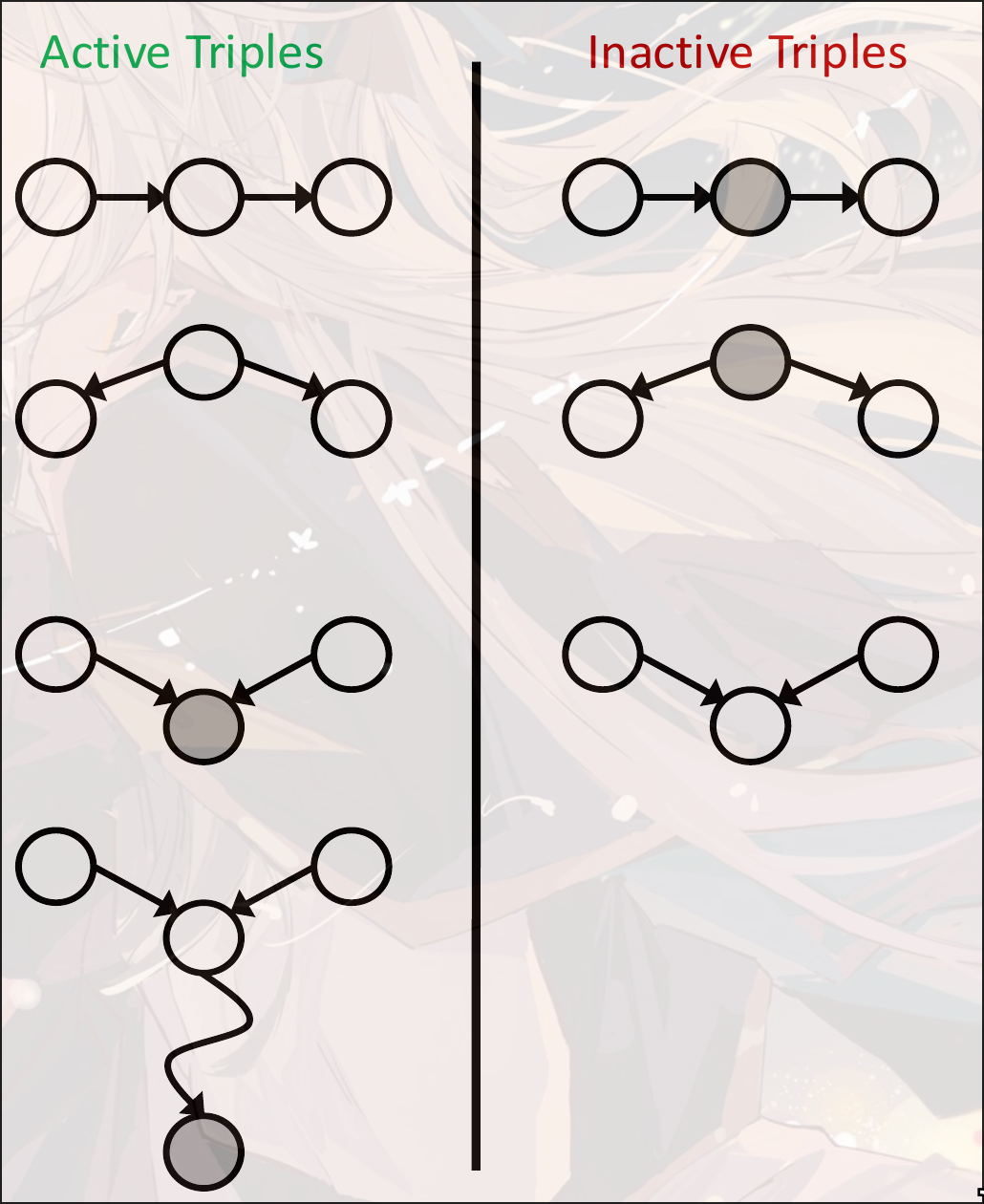 灰色节点表示是given nodes, 即给定的条件(或者说block的nodes)
灰色节点表示是given nodes, 即给定的条件(或者说block的nodes)
这里的Active Triple表示dependent, Inactive Triple表示Conditional Independent
判断两个节点是否是条件独立, 那么可以看这条路径是否是Inactive的.
查询是否条件独立的编程思想:
- 第一层循环遍历所有的路径
- 第二层循环遍历所有的Triple
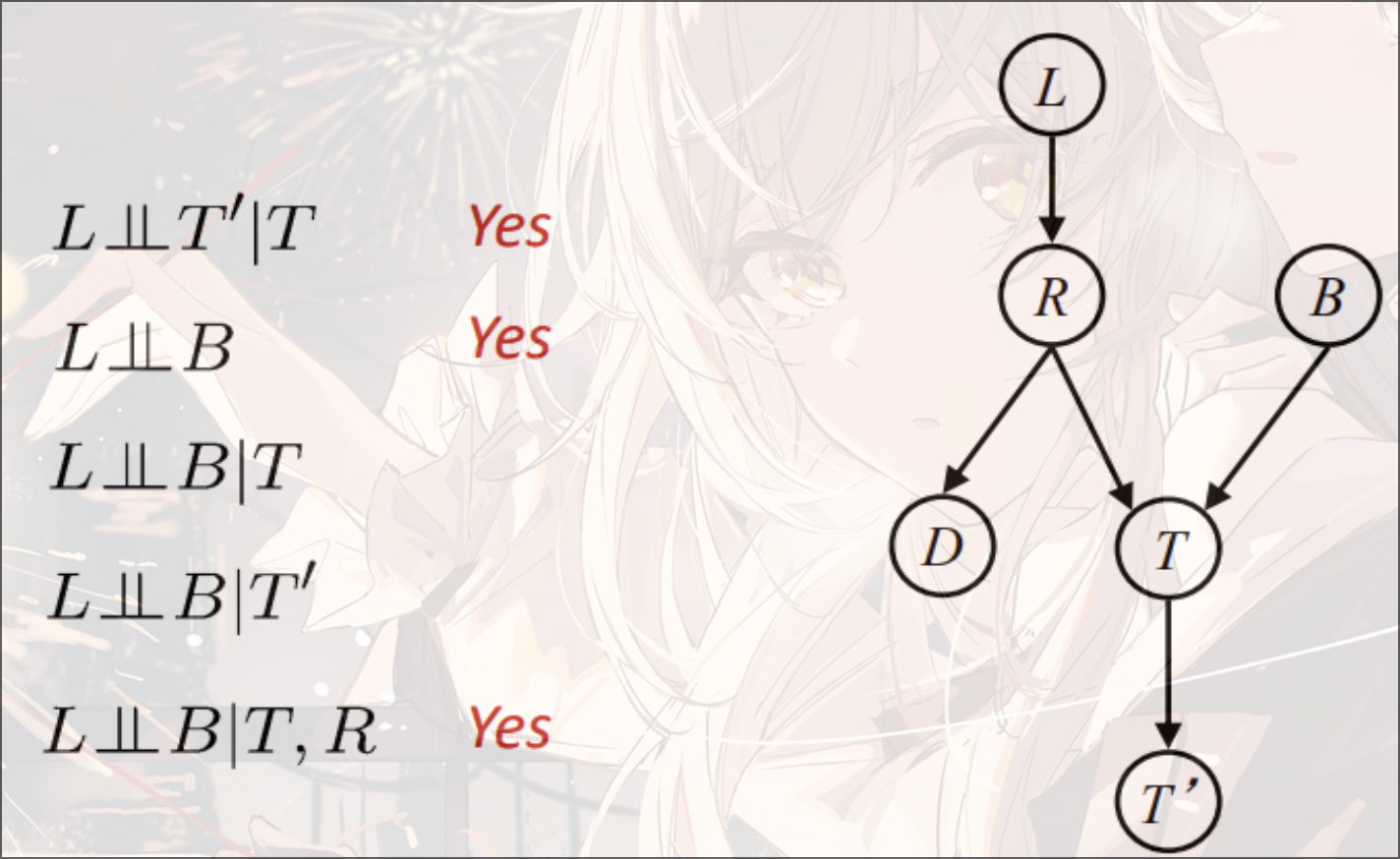
和节点有两个路径, 只有第二条能够全部Inactive
详情参考
D-separate
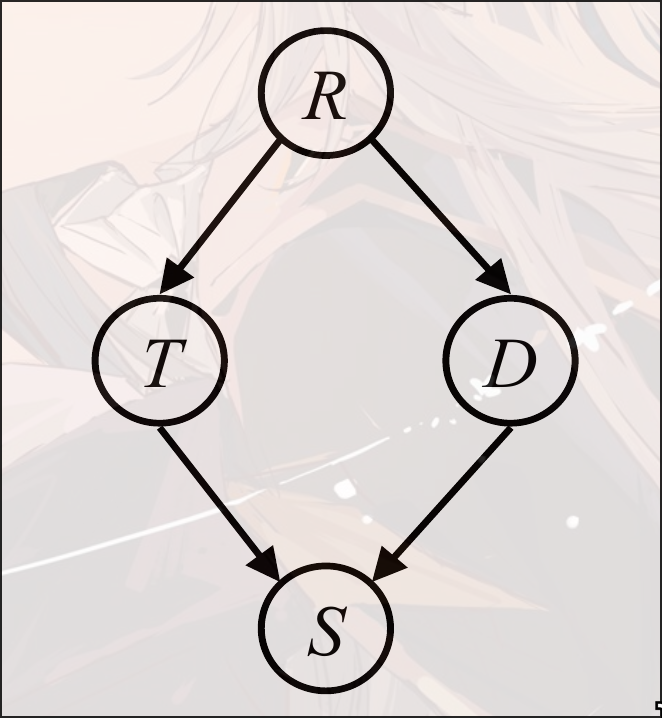
graph TB X-->Y-->Z M-->N M-->P A-->B C-->B这个时候,有三种情况:
- 第一种原来是条件不独立,给定之后变成条件独立
- 第二种原来条件不独立,给定后条件独立
- 第三种原来条件独立,给定之后条件不独立
可以认为,两者之间如果有一条通路,那么就算是条件独立。但是注意第三种,给定之后不是将通路打断,而是把断掉的通路合成
Link to original
e.g.
Node Ordering
每一个模型的假设是不同的, 即可以认为是也可以认为是
但是每一种假设会有不同的计算复杂度和不同的空间复杂度
如果Bayes Network建模的是因果关系, 那么会高效很多
Markov Network
可以看作是无向图+势函数的结合
Bayes Network是有向无环图来建模, Markov Network是无向有环图来定义的
Clique: 一个完全图(全连接)
Maximal Clique: 最大的全连接的图
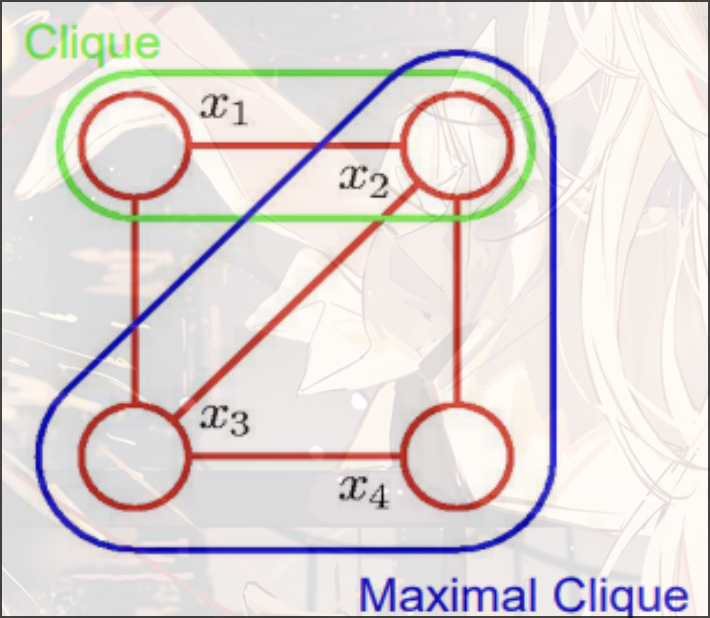
定义势函数针对Clique(或者Maximal Clique).
对于联合概率, 与势函数的乘积成比例:
, 其中是归一化系数
Markov Blanket: 所有与该节点直接相连的节点组成Markov Blanket
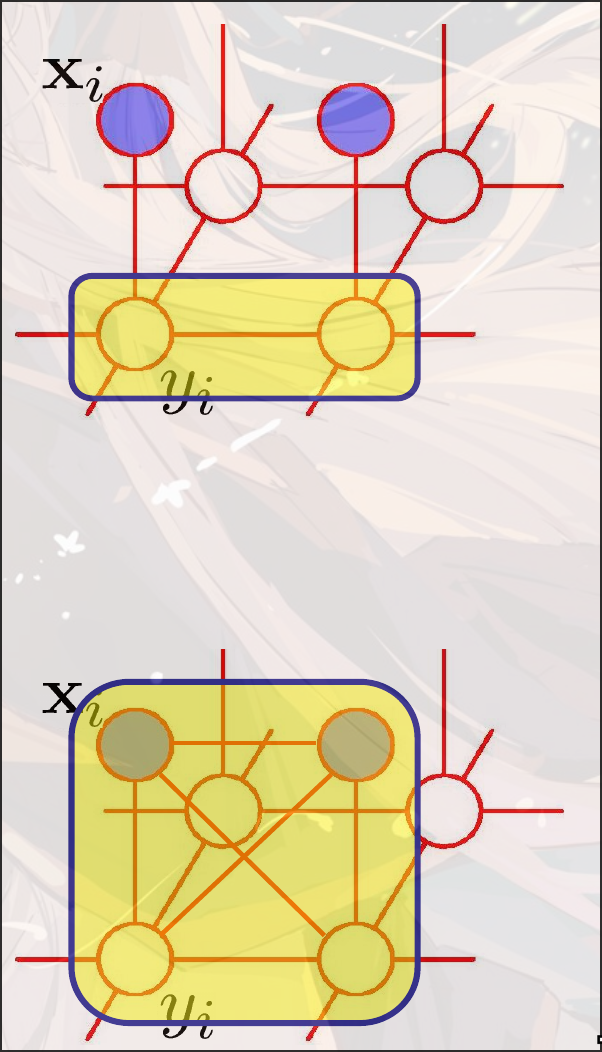
e.g.
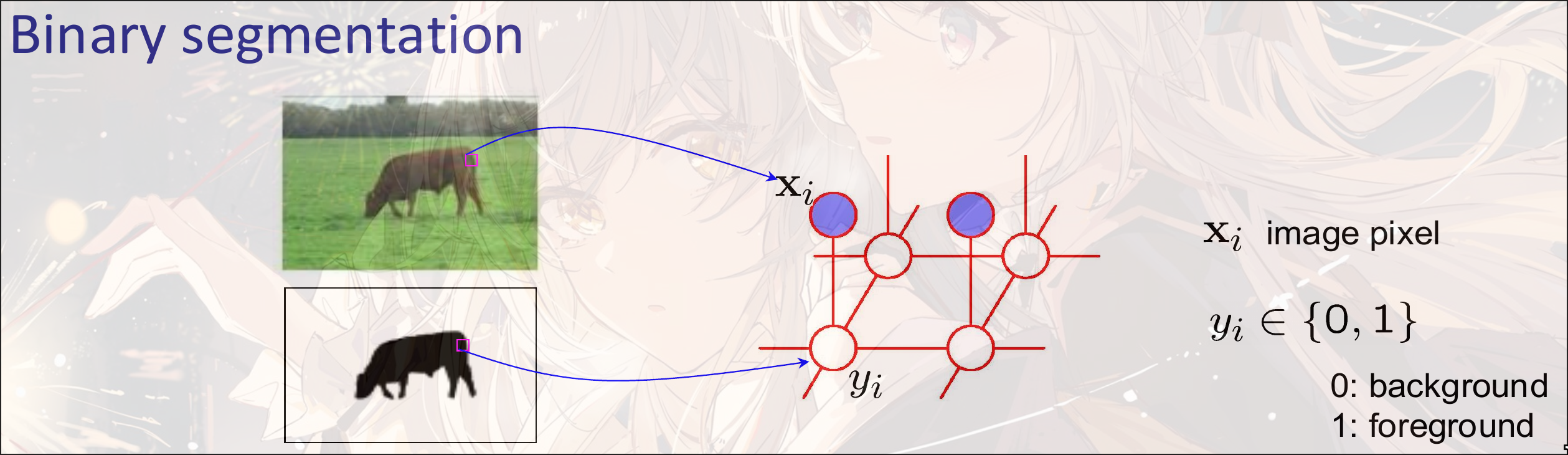
定义每个pixel , 定义pixel对应是否是想要的分类
定义势函数 where is feature vector
定义势函数表示相邻的两个点之间更可能是相同的分类
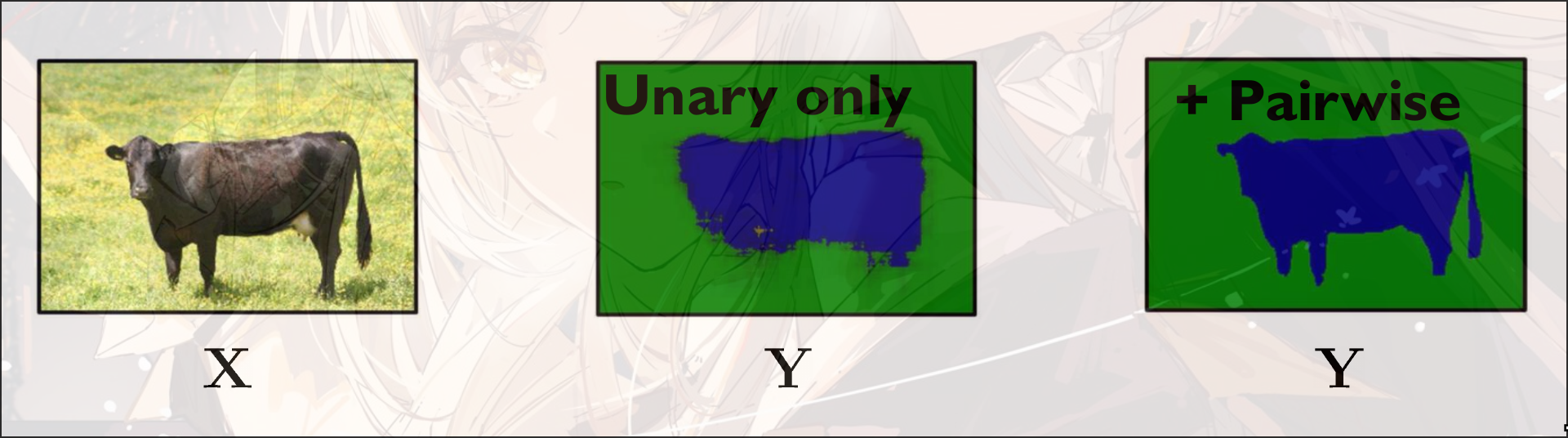
如果有更复杂的网络结构, 那么分类的准确率会更大
Convert Bayes Network to Markov Network
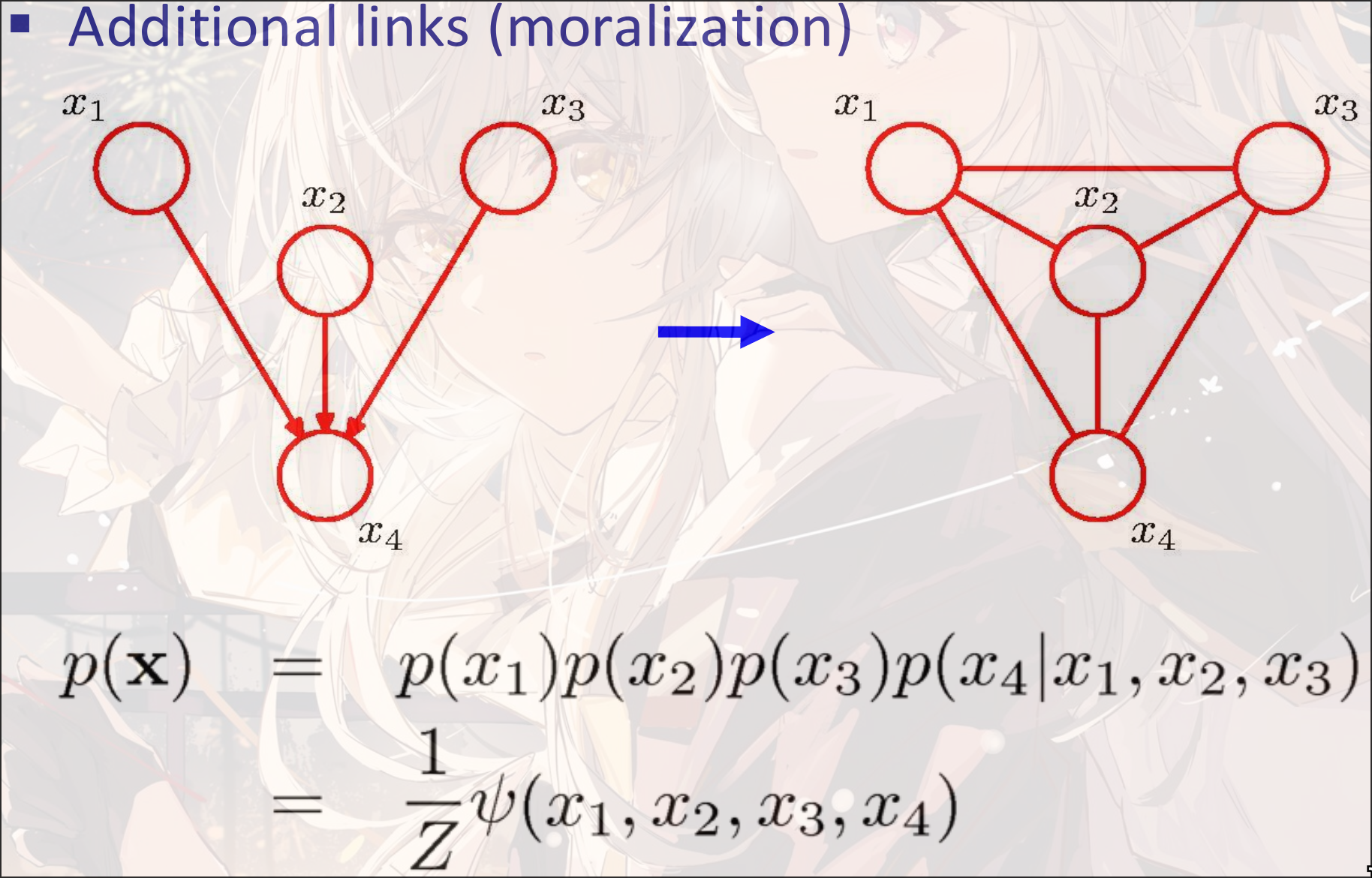
Moralization:
Bayes Network中, 相关的关系不一定体现在边的连接上. 但是在Markov Network中, 只有相连的两个节点才会有关系. 所以在转换的过程中, 需要把相关的两个点添加边连接
Steps:
- Moralization
- Construct potential functions from CPTs
Bayes Network和Markov Network编码了同样的分布
但是并不是编码相同的条件独立性
Tip
如, 在第二张图中, 我们可以认为Markov Network的建模中, 共同影响.
但是Bayes Network中, 不能影响
认为Bayes Network和Markov Network更接近于谓词逻辑PL(相较于一阶谓词逻辑FOL)
可以认为BN和MN是带有概率的拓展PL
CRF Conditional Random Field
生成式模型: 建模一个分布:
- Bayes Network和Markov Network都是Generative Model
判别式模型: 只建模, 不建模
- CRF, Image Segmentation
CRF的概率:
applications:
- NLP
- Pos tagging
- Named entity recognize
- Syntactic parsing
- CV
- Image Segmentation
- Posture Recognize