Ch2.Geometry_of_Linear_Programming

Geometry of linear programming

Polyhedra and convex set

Definition

1. Polyhedron是一个集合$\{\mathbf{x}\in {\mathbb{R}}^n|\mathbf{Ax}\ge \mathbf{b}\},\mathbf{A}\in {\mathbb{R}}^{m\times n},b\in {\mathbb{R}}^n$
2. 如果一个集合$S\subset {\mathbb{R}}^n$存在一个常量$K$满足所有$S$中的元素的所有components的绝对值都小于等于$K$, 那么我们称$S$是有界的(bounded)
3. 如果一个向量$\mathbf{a}\in {\mathbb{R}}^n$, 一个标量$b$, 那么
   • $\{\mathbf{x}\in {\mathbb{R}}^n|{\mathbf{a}}^{\top }\mathbf{x}=b\}$称为超平面(hyperplane)
   • $\{\mathbf{x}\in {\mathbb{R}}^n|{\mathbf{a}}^{\top }\mathbf{x}\ge b\}$称为半空间(halfspace)

之前的feasible set中有提到可以将所有的约束规约成$\mathbf{Ax}\ge \mathbf{b}$的形式, 那么我们可以把Polyhedron看成一个feasible set. 相似的, 我们可以将$\{\mathbf{x}\in {\mathbb{R}}^n|\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge 0\}$当成Polyhedron的标准形式

超平面hyperplane可以看成是有界(bounded)的半空间.

hyperplane的表达中的向量$\mathbf{a}$可以认为是该plane的法向量. 假设该平面与法向量$\mathbf{a}$的交点是${\mathbf{x}}_0$, 那么对于任意一个非${\mathbf{x}}_0$的点$\mathbf{x}$, 都有

$${\mathbf{a}}^{\top }(\mathbf{x}-{\mathbf{x}}_0)=0\Rightarrow {\mathbf{a}}^{\top }\mathbf{x}-{\mathbf{a}}^{\top }{\mathbf{x}}_0=0\Rightarrow {\mathbf{a}}^{\top }\mathbf{x}={\mathbf{a}}^{\top }{\mathbf{x}}_0\Rightarrow {\mathbf{a}}^{\top }\mathbf{x}=\mathbf{b}$$

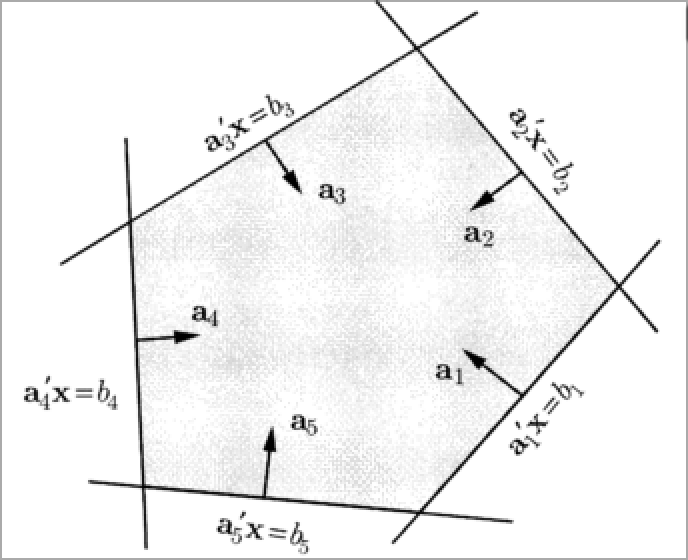
上图是一个polyhedron $\{\mathbf{x}\in {\mathbb{R}}^2|{\mathbf{a}}_i^{\top }\mathbf{x}\ge {\mathbf{b}}_i,i=1,2,3,4,5\}$

Convex Set

Definition

1. 对于一个集合$S$, 如果有$\mathbf{x},\mathbf{y}\in S$满足$\lambda \mathbf{x}+(1-\lambda )\mathbf{y}\in S,\lambda \in [0,1]$, 那么我们称$S$为凸集(convex set)
2. 假设有一组向量${\mathbf{x}}_1,\cdots ,{\mathbf{x}}_n$, 有对应的一组和为$1$的标量${\lambda }_1,\cdots ,{\lambda }_n,s.t.{\sum }_i{\lambda }_i=1$.
   • 我们称${\sum }_{i=1}^n{\lambda }_i{\mathbf{x}}_i$为convex combination
   • 上述所有向量${\mathbf{x}}_i$的**凸面体(convex hull)**即为所有的向量的convex combination组成的集合

注意到$\lambda \mathbf{x}+(1-\lambda )\mathbf{y}$实际上是$\mathbf{x}$和$\mathbf{y}$的加权平均, 是$\mathbf{xy}$连线上的一个分割点. convex set就是判断这条线段是否也在集合中

Theorem

1. convex set的交集(intersection)还是convex set
2. 每一个polyhedron都是convex set
3. 一个convex set中有限元素的convex combination还是属于该convex set
4. 有限个向量的convex hull是一个convex set

Extreme points, vertices, and basic feasible solution

Definition

假设$P$是多面体Polyhedron

1. 如果一个向量$\mathbf{x}\in P$无法在$P$中找到两个向量$\mathbf{y},\mathbf{z}\in P$满足$\lambda \mathbf{y}+(1-\lambda )\mathbf{z}=\mathbf{x},\lambda \in [0,1]$, 那么我们称这个向量$\mathbf{x}$为极点(extreme point)
2. 如果一个向量$\mathbf{x}\in P$, $\exists \mathbf{c}$满足${\mathbf{c}}^{\top }\mathbf{x}<{\mathbf{c}}^{\top }\mathbf{y},\forall \mathbf{y}\in P,\mathbf{y}\ne \mathbf{x}$, 那么我们称向量$\mathbf{x}$为顶点(vertex)

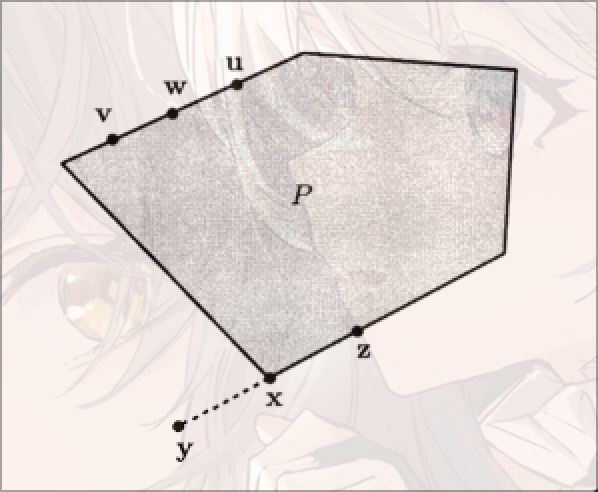
向量$\mathbf{x}$是无法使用两个都在$P$内的点表示的, 但是$\mathbf{x}$本是是属于$P$的.

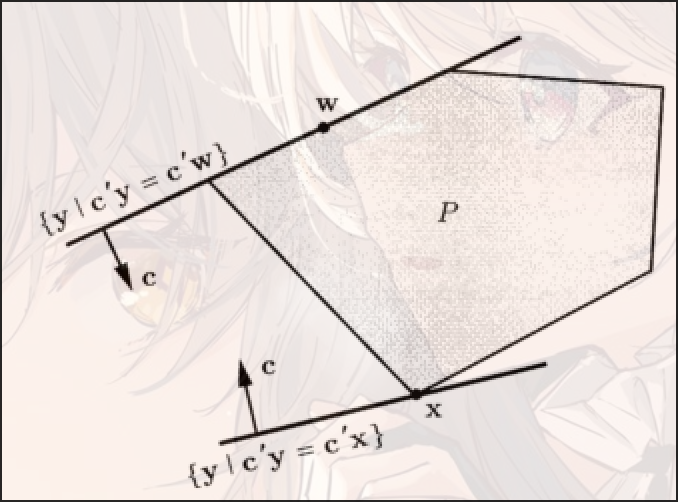
Definition

1. 如果一个向量${\mathbf{x}}^{\ast }$满足对于某些$i\in M_1,M_2,M_3,{\mathbf{a}}_i^{\top }\mathbf{x}=b_i$, 那么我们称对应的约束条件为积极约束(active constrains)
2. 对于一个Polyhedron $P$, 通过等式和不等式来约束. 假设有一个向量${\mathbf{x}}^{\ast }\in {\mathbb{R}}^n$,
   • 如果所有的等式约束都是积极的, 并且有$n$个约束是线性独立的, 那么我们称向量${\mathbf{x}}^{\ast }$为基础解(basic solution)
   • 若${\mathbf{x}}^{\ast }$是basic solution并满足所有的约束, 那么我们称这个向量为基本可行解(basic feasible solution)

如果积极约束有$n$个, 对应$n$个未知变量, 那么如果这$n$个线性方程是线性独立的, 那么这个线性规划系统有解

Theorem

假设向量${\mathbf{x}}^{\ast }\in {\mathbb{R}}^n$, 集合$I=\{i|{\mathbf{a}}_i^{\top }\mathbf{x}=b_i\}$是${\mathbf{x}}^{\ast }$的积极约束的下标, 那么下列说法是等价的(知一推其他)

1. 存在$n$个向量, 属于集合$\{{\mathbf{a}}_i^{\top }|i\in I\}$中, 是线性独立的
2. 所有$\{{\mathbf{a}}_i|i\in I\}$中的向量能够张成(span)整个${\mathbb{R}}^n$空间, 也就是说, 所有的${\mathbb{R}}^n$中的向量可以使用${\mathbf{a}}_i$的线性组合表示出
3. 线性系统${\mathbf{a}}_i^{\top }\mathbf{x}=b_i,i\in I$有唯一解

或者说是约束是线性独立(linear independent)的, 即${\mathbf{a}}_i$是linear independent的.

现在定义corner point的定义: 存在$n$个linear independent的active constrains的feasible solution. 通过寻找$n$个linear independent的active constrains, 我们有一个unique的解${\mathbf{x}}^{\ast }$, 但是这个不一定是feasible的, 因为可能会违反inactive constrains

Definition

假设Polyhedron $P$被线性等式和不等式定义, 假设${\mathbf{x}}^{\ast }$是$P$中的一个元素

1. 若满足: 1. 所有等式均为active solution 2. 在所有对${\mathbf{x}}^{\ast }$的constrains中, 有$n$个是linear independent的. 那么我们称${\mathbf{x}}^{\ast }$是基本解(basic solution)
2. 若${\mathbf{x}}^{\ast }$是basic solution, 并且满足所有的constrains, 那么我们称${\mathbf{x}}^{\ast }$为基本可行解(basic feasible solution)

如果只有$m$个constrains定义Polyhedron, 并且$m<n$, 那么可以认为这个Polyhedron没有basic solution或者basic feasible solution

Theorem

假设非空的Polyhedron $P$, 假设${\mathbf{x}}^{\ast }\in P$, 那么下列条件是等价的:

1. ${\mathbf{x}}^{\ast }$是vertex
2. ${\mathbf{x}}^{\ast }$是extreme point
3. ${\mathbf{x}}^{\ast }$是basic feasible solution

推论: 假设有finite linear inequality constrains, 那么有finite basic or basic feasible solution

Adjacent basic solution

两个${\mathbb{R}}^N$上的不同的basic solution, 如果有$n-1$个linear equality constrains共同active, 那么我们称这两个basic solution为adjacent的.

如果两个adjacent的basic solution都是feasible的, 那么这两个点的连线称为feasible set的边(edge)

Polyhedra in standard form

假设Polyhedron $P=\{\mathbf{x}\in {\mathbb{R}}^n|\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge 0\}$, 其中$\mathbf{A}\in {\mathbb{R}}^{m\times n}$, $m$是行数, 表示equality约束的个数. 假设$\mathbf{A}$的$m$行都是linear independent的, 由于每一行都是$n$维的, 我们可以认为说$m\le n$(为了保证线性独立). 那么我们可以说当$P$非空时, 可以丢弃$A$的线性相关行的冗余约束.

对于任何的basic solution, 都有$n$个linear independent active constrains. 此外, 如果要满足约束$\mathbf{Ax}=\mathbf{b}$, 那么这提供了$m$个active constrains. 由于我们假设了$m\le n$并且这$m$个约束都是linear independent的, 我们还需要$n-m$个与$\mathbf{Ax}=\mathbf{b}$提供的$m$个约束也独立的线性约束. 因此我们会选择$n-m$个变量$x_i$创建等式$x_i=0$, 即满足约束$\mathbf{x}\ge 0$. 为了让$x_i=0$也是linear independent, 我们对$x_i$的选择是有特定方案的.

Definition

1. 考虑$\mathbf{Ax}=\mathbf{b}$和$\mathbf{x}\ge 0$, 假设$\mathbf{A}$是row-independent的. 假设basic solution $\mathbf{x}\in {\mathbb{R}}^n$, 当且仅当有$\mathbf{Ax}=\mathbf{b}$时, 存在索引(indices)$B(1),\cdots ,B(m)$, 满足:
   • 列$A_{B(1)},\cdots ,A_{B(m)}$是linear independent的
   • 如果$i\ne B(1),\cdots ,B(m)$, 那么$x_i=0$

那么对于Standard Form的Polyhedron可以用这个方式求解:

1. 找$m$个linear independent column: ${\mathbf{A}}_{B(1)},\cdots ,{\mathbf{A}}_{B(m)}$
2. 令$x_i=0,\forall i\ne B(1),\cdots ,B(m)$
3. 解方程$\mathbf{Ax}=\mathbf{b}$, 求解$x_{B(1)},\cdots ,x_{B(m)}$

如果上述方法构建的basic solution是非负的, 那么我们可以认为是一个feasible basic solution.

变量$x_{B(i)}$称为基本变量(basic variables), 其他的是非基本变量(nonbasic). 我们称列$A_{B(i)}$为基本列(basic column), 并且他们是linear independent的, 因此他们组成了${\mathbb{R}}^m$的一组基. 我们假定不同的基有不同的索引, 但是如果顺序不同不认为是不同的基.

将$m$个基本列组合在一起, 我们获得了一个$\mathbf{B}\in {\mathbb{R}}^{m\times m}$, 称为基矩阵, 是可逆的, 因为所有column linear independent, 因此是满秩的.

$$\mathbf{B}=\left[\begin{array}{ccc}|& \cdots & |\\ A_{B(1)}& \cdots & A_{B(m)}\\ |& \cdots & |\end{array}\right],{\mathbf{x}}_B=\left[\begin{array}{c}{x}_{B(1)}\\ ⋮\\ x_{B(m)}\end{array}\right]$$

解基本方程${\mathbf{Bx}}_B=\mathbf{b}$有${\mathbf{x}}_B={\mathbf{B}}^{-1}\mathbf{b}$

假设有${\mathbf{A}}_{B(p)}={\mathbf{A}}_{B(q)}$, 那么两组基$\{\cdots ,B(p),\cdots \}$和$\{\cdots ,B(q),\cdots \}$是完全相同的, 但是不是相同的基, 因为indices不同

Correspondence of bases and basic solutions

一组基唯一确定一个基本解. 但是不同的基可能确定了相同的基本解.

Adjacent basic solution and adjacent base

相似的, 如果两组bases共享除了一个basic column以为所有的basic column, 我们称这两组bases为相邻的

相邻的basic solution总是从相邻的bases中获得. 同样, 如果相邻的bases获取不同的basic solution, 那么也是相邻的.

The full row rank assumption on $\mathbf{A}$

Theorem

假设有非空Polyhedron $P=\{\mathbf{x}|\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge 0\}$, $\mathbf{A}\in {\mathbb{R}}^{m\times n}$, 有${\mathbf{a}}_1^{\top },\cdots ,{\mathbf{a}}_m^{\top }$是$\mathbf{A}$的行向量. 假设$\text{rank}\mathbf{A}=k<m$且行${\mathbf{a}}_{i_1}^{\top },\cdots ,{\mathbf{a}}_{i_k}^{\top }$是linear independent的. 假设有一个Polyhedron $Q=\{\mathbf{x}|{\mathbf{a}}_{i_1}^{\top }\mathbf{x}=b_{i_1},\cdots ,{\mathbf{a}}_{i_k}^{\top }\mathbf{x}=b_{i_k},\mathbf{x}\ge 0\}$, 那么可以认为$P=Q$

注意, Q其实是标准形式的, 可以写成$Q=\{\mathbf{x}|\mathbf{Dx}=\mathbf{f},\mathbf{x}\ge 0\}$, 其中$\mathbf{D}\in {\mathbb{R}}^{k\times n}$是$\mathbf{A}$的一个子矩阵, $\mathbf{f}\in {\mathbb{R}}^k$是$\mathbf{b}$的$k$维子向量.

因此我们可以得出结论, 只要是非空的feasible set, 那么可以将标准形式的线性规划问题简化为一个等价的具有相同feasible set的标准形式问题, 并且该问题的所有约束都是linear independent的.

Degeneracy

可能会存在有多个active constrains的情况, 但是线性独立的约束最多不超过$n$个. 在这种情况下, 我们有了一个**退化(degeneracy)**的basic solution.

Definition

若一个basic solution $\mathbf{x}\in {\mathbb{R}}^n$的active constrains超过$n$个, 那么我们称这个$\mathbf{x}$是**退化(degeneracy)**的.

在二维空间中, 一个degeneracy的basic solution基本上是三条或以上的直线的交点.

Degeneracy in standard form polyhedra

Definition

标准形式Polyhedron $P=\{\mathbf{x}|\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge 0\},\mathbf{A}\in {\mathbb{R}}^{m\times n}$有basic solution $\mathbf{x}$. 假设$\mathbf{x}$有超过$n-m$个分量为$0$, 那么$\mathbf{x}$是一个degeneracy的basic solution.

Degeneracy is not a purely geometric property

在一个特定标准形式表示下degeneracy的basic feasible solution在另一个表示下可能是非退化的。然而，可以证明，如果一个basic feasible solution在一个特定的标准形式表示下是退化的，那么它在同一多面体的每个标准形式表示下都是退化的

Existence of extreme points

Definition

一个Polyhedron $P\subset {\mathbb{R}}^n$, 如果存在一个向量$\mathbf{x}\in P$和一个非$0$向量$\mathbf{d}\in {\mathbf{R}}^n$, 满足$\mathbf{x}+\lambda \mathbf{d}\in P$对于任意的标量$\lambda$, 那么$P$包含一条直线.

Theorem

假设$P=\{\mathbf{x}\in {\mathbb{R}}^n|{\mathbf{a}}_i^{\top }\mathbf{x}\ge b_i,i=1\cdots ,m\}$, 下列说法是等价的:

1. $P$至少有一个extreme point
2. $P$不包含直线
3. 存在来自${\mathbf{a}}_i,i=1,\cdots ,m$的$n$个向量是linear independent的

Corollary

每个非空有界的Polyhedron至少有一个basic feasible solution

Optimality of extreme points

Theorem

考虑在Polyhedron $P$上最小化${\mathbf{c}}^{\top }\mathbf{x}$的线性规划问题. 假设Polyhedron至少有一个extreme point, 至少有一个最优解. 那么$P$上的extreme point就是${\mathbf{c}}^{\top }\mathbf{x}$的最优解

如果不存在最优解, 那么最小值一定是$-\infty$, 否则最优解一定是其中一个extreme points

Corollary

一个线性规划求解${\mathbf{c}}^{\top }\mathbf{x}$的最小值, 要么是$-\infty$, 要么存在一个最优解

Representation of bounded polyhedra

Theorem

一个非空的有界的(bounded) polyhedron $P$是其所有的extreme points组成的convex hull