SI120

数理逻辑

命题 - Proposition

• 定义: 一个陈述句, 不是真就是假

• 一般用小写字母表示命题

• 可以是一个变量, 只能是True或者False的变量(Boolean)

• 例子

  • $\sqrt{2}$ is irrational $\Rightarrow$ True
  • $1+1=2$ $\Rightarrow$ True
  • $1+1=0$ $\Rightarrow$ False
  • 每个大于二的整数都是两个质数之和 $\Rightarrow$ 是命题, 但是至今为止不知道正确与否(哥德巴赫猜想)
  • What time is it? $\Rightarrow$ 不是命题
  • Do not smoke! $\Rightarrow$ 不是命题
  • $x+1=2$ $\Rightarrow$ 不是命题, 返回值有可能是真有可能是假, 值是不确定的. (这是不完整的陈述句)

种类

• 简单命题 - Simple Proposition
  • $\sqrt{2}$是无理数
• 复合命题 - Compound Proposition
  • 2是有理数而且$\sqrt{2}$是无理数 (能够分解成两个简单命题)
• 命题常项 - Proposition Constant
  • 每个大于二的整数都可以分解成两个质数之和
• 命题变项 - Proposition Variable
  • 用变量表示的(p,q,r,s,…, 是小写字母)
  • 真值直到分配一个命题常项之后才会得出
• 命题逻辑 - Proposition Logic

真值表 - Truth Table

• 定义: F是对于n个命题变项的WWFs, 对于F的一个真值指派(Truth Assignment)是映射$\alpha :\{p_1,...,p_n\}\to \{T,F\}$.

例子: $A=p\vee \neg p$

$p$	$\neg p$	$A$
T	F	T
F	T	T

运算

否定 - Negation

• 定义: 对于命题p的否定是”如果不是p”
• "$\neg p$"读作”非p”, “not p”

真值表:

p	$\neg$p
T	F
F	T

例子:

• p = “雪是白的”
• $\neg$p = “雪不是白的”
• 但是不等于”雪是黑的”, 因为还可能是其他颜色, 红的黄的绿的蓝的…

合取 - Conjunction

• 定义: 对于p, q的合取是”p和q”

p	q	p$\wedge$q
T	T	T
T	F	F
F	T	F
F	F	F

析取 - Disjunction

• 定义: p或q

p	q	p$\vee$q
T	T	T
T	F	T
F	T	T
F	F	F

隐含 - Implication

• 定义: 如果p, 那么q

真值表:

p	q	p$\to$q
T	T	T
T	F	F
F	T	T
F	F	T

例子:

• p=“你的了100分”, q=“你获得了A+”
• p$\to$q: “如果你得了100分, 那么你就会获得A+”

只有真推假的时候真值是假: $(p,q)=(T,F)$时才是假

条件没有完成的时候, 前置条件变成了未知状态, 所以认为在这种情况下, 所有的情况都按照真处理.

等值 - Bi-Implication

• 定义: p当且仅当q

真值表:

p	q	p$\leftrightarrow$q
T	T	T
T	F	F
F	T	F
F	F	T

只有$(p,q)=(T,F)or(F,T)$的时候真值才是假

运算优先级 - Precedence of Logical Operators

优先看$()$里面的

$\neg ,\wedge ,\vee ,\to ,\leftrightarrow$降序

同级左到右

合式公式 - Well-Formed Formulas

• 定义(递归定义):

  • 命题常项和命题变项是WWF

  • 如果A是WWF, 那么$\neg$A也是WWF

  • 如果A,B是WWF, 那么(A$\wedge$B),(A$\vee$B),(A$\to$B),(A$\leftrightarrow$B)是WWF

  • 用有限个运算符拼接WWF的式子, 结果也是WWF

• 例子:

  • ((p$\wedge$q)$\vee$(r)) 是
  • $\neg$p$\vee$ 不是(少项)
  • (p$\vee$q)$\neg$r 不是

构建一颗算符树, 是否能构成一颗完整的树(不能是森林)

$\begin{array}{ccc}\neg -r& & \\ & |& -p\\ \vee -& |& \\ & |& -q\end{array}$

(第三个, 不是完整的树, 所以不是WWF)

将自然语言转换为WWF

• 先找出所有简单命题, 用p,q,r,…表示
• 用逻辑连接符将简单命题连接起来

例子:

• “雪不是黑的”
  • p: “雪是黑的”
  • $\neg$p
• “$e^{\pi }>{\pi }^e$当且仅当$\pi >e\ln \pi$”
  • p: "$e^{\pi }>{\pi }^e$", q: "$\pi >e\ln \pi$"
  • p$\leftrightarrow$q

一些比较离谱的东西:

• ${\sqrt{2}}^{\sqrt{2}}$是无理数或有理数
  • p: “${\sqrt{2}}^{\sqrt{2}}$是有理数”, q: “${\sqrt{2}}^{\sqrt{2}}$是无理数”
  • 有两种连接方法:
    • 或者(可能都成立): p$\vee$q
    • 互斥的: (p$\wedge \neg$q)$\vee$($\neg$p$\wedge$q)

1. “A当且仅当B不来的时候来, 但是如果B来了, C不来, D来”
2. “一个A来的充分条件(sufficient condition)是B不来, C和D至少有一个来”

• p: “A来”, q: “B来”, r: “C来”, s: “D来”
• (p$\leftrightarrow \neg$q)$\wedge$(p$\to$($\neg$r$\wedge$s)) : 判断谁来了这种情况成不成立(来了就是True; 表达式的真值成立就是True, 不成立就是False)
• ($\neg$b$\to$(c$\vee$d))$\to$p : 跟上面一样, 是对第二条的翻译. 但是和上面的那句不等价, 因为还有一个限制条件: C和D至少来一个. 那么A来B不来CD都不来的情况满足上面的式子但是不满足下面的.

WWF的类型

• 重言式 - Tautology: WWF的所有表达式的值都是True
• 矛盾式 - Contradiction: WWF的所有表达式都是False
• 可能式 - Contingency: 既不是重言式也不是矛盾式
• 可满足的 - Satisfiable: 一个WWF至少有一种真值指派

代入法则:

假设B是一个重言式, A是任意的命题变项, 将A代入B的结果也是一个重言式.

• 例子:
• $p\vee \neg p$ is tautology, then $(q\wedge r)\vee \neg (q\wedge r)$ is also a tautology

WWF本身可以看作一个映射(函数), 然后将其中的一个变量替换成一个函数(类似于复合函数), 就是代入法则

逻辑等价 - Logically Equivalent

• 定义: 如果A和B是变量$p_1,p_2,...,p_n$的WWF, A和B逻辑等价当且仅当A,B有相同的真值指派在任意的命题变项的真值指派下
• 定理: 如果A,B是逻辑等价的, 那么$A\leftrightarrow B$是重言式
• 定理: $A\equiv B,B\equiv C\Rightarrow A\equiv C$

想要证明, 可以用穷举法.

替换规则 - Rule of Replacement

1. 将F的子公式替换为逻辑等价形式并简化

Ex.

$$\begin{array}{rl}& p\to (p\vee \neg q\vee r)\\ \equiv & \neg p\vee (p\vee \neg q\vee r)\\ \equiv & (\neg p\vee p)\vee \neg q\vee r\\ \equiv & T\vee \neg q\vee r\\ \equiv & T\end{array}$$

Ex.

$$\begin{array}{rl}& \neg ((p\vee q)\wedge \neg p\to q)\\ \equiv & \neg (\neg ((p\vee q)\wedge \neg p)\vee q)\\ \equiv & ((p\vee q)\wedge \neg p)\wedge \neg q\\ \equiv & (p\vee q)\wedge \neg (p\vee q)\\ \equiv & F\end{array}$$

2. 令$A^{-1}(T)$为满足A为真值的真值派遣的集合，则当且仅当$A^{-1}(T)=B^{-1}(T)$时，有$A\equiv B$

Ex. $P\wedge Q\equiv Q\wedge P$, $A=P\wedge Q,B=Q\wedge P$

• $A=T\text{ 当且仅当 }(P,Q)=(T,T)\Rightarrow A^{-1}(T)=\{(T,T)\}$
• $B=T\text{ 当且仅当 }(P,Q)=(T,T)\Rightarrow B^{-1}(T)=\{(T,T)\}$
• $A^{-1}(T)=B^{-1}(T)\Rightarrow A\equiv B$

重言蕴含 - Tautological Implications

• 定义: 令$A$和$B$是命题变项$p_1,p_2,...$的WWFs, 当每一个真值指派使得$A$是真的时候$B$也是真, 那么称$A$是$B$的重言蕴含
• 写作$\Rightarrow$

定理:

• $A\Rightarrow B$当且仅当 $A\to B$是一个重言式

• $A\Rightarrow B$当且仅当$A\wedge \neg B$是矛盾式

名字	重言蕴含
合取	$(P)\wedge (Q)\Rightarrow P\wedge Q$
化简	$P\wedge Q\Rightarrow P$
附加	$P\Rightarrow P\vee Q$
假言推理	$P(P\to Q)\Rightarrow Q$
拒取	$\neg Q\wedge (P\to Q)\Rightarrow \neg P$
析取三段论	$\neg P\wedge (P\vee Q)\Rightarrow Q$
假言三段论	$(P\to Q)\wedge (Q\to R)\Rightarrow (P\to R)$
归论	$(P\vee Q)\wedge (\neg P\vee R)\Rightarrow (Q\vee R)$

证明拒取:

$$\begin{array}{rl}A& =\neg Q\vee (P\to Q),B=\neg P\\ A\to B& \equiv \neg (\neg Q\vee (P\to Q))\vee \neg P\equiv (Q\vee \neg (P\to Q))\vee \neg P\\ & \equiv (\neg P\vee Q)\vee \neg (P\to Q)\equiv T\end{array}$$

证明假言三段论:

$$\begin{array}{rl}A& =(P\to Q)\wedge (Q\to R)\\ B& =(P\to R)\\ A\wedge \neg B& \equiv (\neg P\to Q)\wedge (\neg Q\to R)\wedge (P\to \neg R)\end{array}$$

论证 - Argument

• 定义: 一个论证是命题的语句

结论(conclusion): 最终命题

假设(Premises): 其他命题

有效(Valid): 假设能够推导出结论 the truth of premises implies that of the conclusion

证明(Proof): 一个有效的论证推出结论 a valid argument that establishes the truth if a conclusion

• 例子:
  • 如果$\{2^n\}$是收敛的, 那么$\{2^n\}$有收敛子列

论证形式 - Argument Form

• 定义: 论证形式是一种格式
• 就是可以把任意的命题带入到论证形式中, 如果论证形式是正确的, 那么将任意的命题代入, 那么论证都是正确的.

有效(Valid): 将任何的命题都替换成命题变量, 从论证形式的真值推出结论的真值

推理规则: 有效的论证形式.

例子:

• $p\to q$
• $p$
• $q$
• valid

p	q	$p\to q$
T	T	T
T	F	F
F	T	T
F	F	T

(T, F) 时是个无效的(invalid)论证

• 例子:
  • p: $\{(-1{)}^n\}$ is convergent
  • q: $\{(-1{)}^n\}$ has a convergent subsequence
  • $p\to q$: if $\{(-1{)}^n\}$ is convergent, then it has a convergent

构建论证 - Building Arguments

给定假设$P_1,P_2,\cdots ,P_n$, 推出结论$Q$, 就是$P_1\wedge P_2\wedge \cdots \wedge P_n\Rightarrow Q$

对应关系:

名字	操作
假设(Premises)	given formulas
结论(Conclusion)	Quote the intermediate formula that have been deducted.
替换规则(Rule of replacement)	Replace a formulas with a logical equivalent formulas
Rules of Inference	Deduct a new formula with a tautological implication.
Rule of substitution	Deduct a formula from a tautology.

谓词 - Predicate

• 定义: 描述一个满射的属性
• n元谓词: 连接n个个体词(Individuals)的满射的词汇
  • I: “是一个整数” - unary, 一元谓词
  • G: “大于” - binary, 二元谓词
• 谓词常项 - Predicate Constant
• 谓词变项 - Predicate Variable: 能表示谓词常项的代表

个体词 - Individual

• 定义: 表示一个对象的词
• 个体域 - Domain: 所考虑的个体词的集合

例子:

• $\sqrt{1+2\sqrt{1+3\sqrt{...}}}$ is an integer
• 个体常项 Individual Constant: $\sqrt{1+2\sqrt{1+3\sqrt{...}}}$
• 个体变项 Individual Variable: $x,y,z,...$

从谓词到命题

命题函数 - Propositional function

• 定义:$P(x_1,\dots ,x_n)$, P是一个n元谓词

个体词函数 - Function of Individuals

• 定义: 在个体域上的映射
• 例子:
  • $f(x)=x$的父节点
  • $p=D(f(Alice))$

量词修饰的命题

全称量化 - Universal Quantifier

• 定义: 令$P(x)$是一个命题函数, 则$P(x)$的全称量化是”所有个体域里的$x$对应的$P(x)$”

• $\forall xP(x)$, 读作”对于任意的$xP(x)$” (“for all $xP(x)$”)

  • "$\forall$"成为全称量词
  • "$\forall xP(x)$" 当且仅当 个体域里所有的$x$对应的$P(x)$都为真时 为真
  • "$\forall xP(x)$" 当且仅当 个体域中存在一个$x_0$对应的$P(x_0)$为假时 为假

• 如果个体域为空, 那么所有的$xP(x)$都为真

存在量化 - Existential Quantifier

• 定义: 令$P(x)$是一个命题函数, 则$P(x)$的存在量化是”所存在一个个体域里的$x_0$对应的$P(x_0)$”

• $\exists x_{0}P(x_0)$, 读作”对任意的$x_{0}P(x_0)$”

  • $\exists$是存在量词
  • $\exists x_{0}P(x_0)$为真, 当且仅当在个体域中存在一个$x_0$使得$P(x_0)$为真
  • $\exists x_{0}P(x_0)$为假, 当且仅当所有个体域中的$x$都能使$P(x)$为假

• 如果个体域为空, 那么所有的$\exists xP(x)$为假

• 如果没有stated, 那么个体词可以是任意的

绑定变量和辖域 - Binding Variables and Scope

• 定义: 如果对于一个个体词有量化词($\exists ,\forall$)修饰, 那么称这个个体词是约束的(bound). 否则, 被称为自由的(free)

  • 例子: $\exists x(x+y=1)$
    • $x$是约束的, $y$是自由的

• 定义: 辖域(scope): 量化词的作用公式

  • 例子: $\exists x(x+y=1)$的辖域是$(x+y=1)$

• 谓词逻辑 - Predicate Logic:

  • 定义: (the area of logic that deals with predicates and quantifiers)

谓词逻辑的良构公式(合式公式) - Well-Formed Formula:

• 变量

  • Propositional constants: T,F, 𝑝, 𝑞, 𝑟, …
  • Propositional variables: 𝑝, 𝑞, 𝑟, …
    • Logical Connectives: ¬,∧,∨, →, ↔
    • Parenthesis: (, )
    • Individual constants: 𝑎, 𝑏, 𝑐, …
    • Individual variables: 𝑥, 𝑦, 𝑧, …
    • Predicate constants: 𝑃,𝑄, 𝑅, …
    • Predicate variables: 𝑃,𝑄, 𝑅, …
    • Quantifiers: ∀, ∃
    • Functions of individuals: 𝑓, 𝑔, …

• 定义:

  • 没有连接的命题变项, 命题常项, 命题函数是WWF
  • 如果$A$是WWF, 那么$\neg A$也是
  • 如果$A,B$是WWF且$A,B$中不存在在一个中有约束但在另一个中没有约束的个体词, 那么$A\wedge B,A\vee B,A\to B,A\leftrightarrow B$都是WWF
  • 如果$A$是WWF, 且个体词$x$在$A$中是自由的, 那么$\exists xA,\forall xA$是WFF
  • WWF可以被上面的四条规则构造

• 例子:

  • $\forall xF(x)\vee G(x),\forall xG(y)$ 不是WFF
  • $\exists x(A(x)\to \forall yB(x,y))$ 是WFF

优先级: 所有的$\exists ,\forall$优先级都大于$\neg ,\wedge ,\vee ,\to ,\leftrightarrow$

• $\exists xF(x)\to G(y)\equiv (\exists xF(x))\to G(y)$

自然语言转换WFF

• 例子:
  • Every irrational number is a real number.
    • For every $x$, if $x$ is an irrational number, then $x$ is a real number.
    • $I(x)$ = “$x$ is an irrational number”
    • $R(x)$ = “$x$ is a real number”
    • Translation: $\forall x(I(x)\to R(x))$

解释 - Interpretation

类似于真值指派

• definition: an interpretation requires one to (remove all uncertainty)

  • assign a concrete proposition to every proposition variable
  • assign a concrete predicate to every predicate variable
  • restrict the domain of every bound individual variable
  • assign a concrete individual to every free individual variable
  • choose a concrete function, if there is any

• 定义: 一个解释需要至少一个:

  • 给每个命题变项分配具体的命题
  • 给每个谓词变量分配具体的命题
  • 限制每个约束个体词的个体域
  • 给每个个体词变量分配具体的个体词
  • 如果有, 那么选择一个具体的函数

• 例子: $\exists xP(x)\to q$

  • $x$的个体域是{Alice,Bob,Eve}
  • $P(x)$是”$x$获得A+的成绩”
  • $q$是”我得了A+”
  • 如果Alice,Bob,Eve中至少有一个得了A+, 那么我获得了A+

WFF的类型 - Type of WFF

1. 普遍有效 - logically valid: 对于任何解释(interpretation)都为真
   • $\forall x(P(x)\vee \neg P(x))$
2. 不可满足 - unsatisfiable: 对于任何解释都为假
   • $\exists x(P(x)\wedge \neg P(x))$
3. 可满足 - satisfiable: 存在一种解释为真
   • 例: $\forall x(x^2>0)$只有在个体域为非零的实数时成立

替换规则 - Rule of Substitution

• 定义: 假设A是重言式, 如果将A所有的命题变项替换成一个WWF的逻辑表达式, 那么得到的表达式也是一个普遍有效的WWF
• 例子: $p\vee \neg p$ is a tautology; hence, $P(x)\vee \neg P(x)$ is logically valid

逻辑等值 - logical equivalent

• 定义: 如果两个WFF在任何解释(interpretation)下都有相同的真值, 那么这两个WFF时逻辑等值的, 写作$A\equiv B$

  • 例: $\forall xP(x)\vee \forall xG(x)\equiv \forall x(P(x)\vee G(x))$

• 定理: $A\equiv B$ 当且仅当 $A\leftrightarrow B$时普遍有效的

• 定理: $A\leftrightarrow B\equiv (A\to B)\wedge (B\to A)$, 即$A\equiv B$当且仅当$(A\to B)\wedge (B\to A)$为普遍成立

德摩根定律 - De Morgan’s Laws for Quantifiers

• 定理: $\neg \forall xP(x)\equiv \exists x\neg P(x)$, $\neg \exists xP(x)\equiv \forall x\neg P(x)$

• 证明(以第一条为例)

  • Show that $\neg \forall xP(x)\to \exists x\neg P(x)$ is valid.
    • Suppose that $\neg \forall xP(x)$ is true in an interpretation, then $\forall xP(x)$ is false in this interpretation
    • There is a $x_0$ such that $P(x_0)$ is false, then the $x_0$ satisfies that $\neg P(x_0)$ is true.
    • Then $\exists x\neg P(x)$ is true.
  • Show that $\exists x\neg P(x)\to \neg \forall xP(x)$
    • Suppose that $\exists x\neg P(x)$ is true in an interpretation, then there is a $x_0$ such that $\neg P(x_0)$ is true.
    • then the $P(x_0)$ is false in this interpretation.
    • $\forall xP(x)$ is false. (因为有一个$x_0$使得$P(x)$是false, 那么任意x推P(x)是错误的)
    • $\neg \forall xP(x)$ is true
  • Q.E.D.

量词分配定律 - Distributive Laws for Quantifiers

• 定理: $\forall x(P(x)\wedge Q(x))\equiv \forall xP(x)\wedge \forall xQ(x)$, $\exists x(P(x)\vee Q(x))\equiv \exists xP(x)\vee \exists xQ(x)$

注意$\forall$对应$\wedge$, $\exists$对应$\vee$

重言蕴含 - Tautological Implications

和前面WWF的重言蕴含是一样的, 只是把重言式换成了普遍成立

只需要排除$T\to F$的情况就好

论证 - Argument

特殊: 引用规则 Rule of Inference

Name	Rule
Universal Instantiation 全称量词消去	$\forall xP(x)\Rightarrow P(a)$ $a$ is any individual in the domain of $x$
Universal Generalization 全称量词引入	$P(a)\Rightarrow \forall xP(x)$ $a$ takes any individual in the domain of $x$
Existential Instantiation 存在量词消去	$\exists xP(x)\Rightarrow P(a)$ $a$ is a specific individual in the domain of $x$
Existential Generalization 存在量词引入	$P(a)\Rightarrow \exists xP(x)$ $a$ tesse a specific individual in the domain of $x$

图论

边:E, 顶点: V, 面: F, 图: G,

Graph - 图

• 定义: a graph G = (V, E) is defined by a nonempty set V of vertices(顶点) and a set E if edges(边), where each edge is associated with one or two vertices(called endpoints(端点) of the edge).

  • 无限图 - Infinite Graph: $|V|=\infty or|E|=\infty$

  • 有限图 - Finite Graph: $|V|<\infty and|E|<\infty$, $|V|$被成为图的阶数(order)(顶点个数)

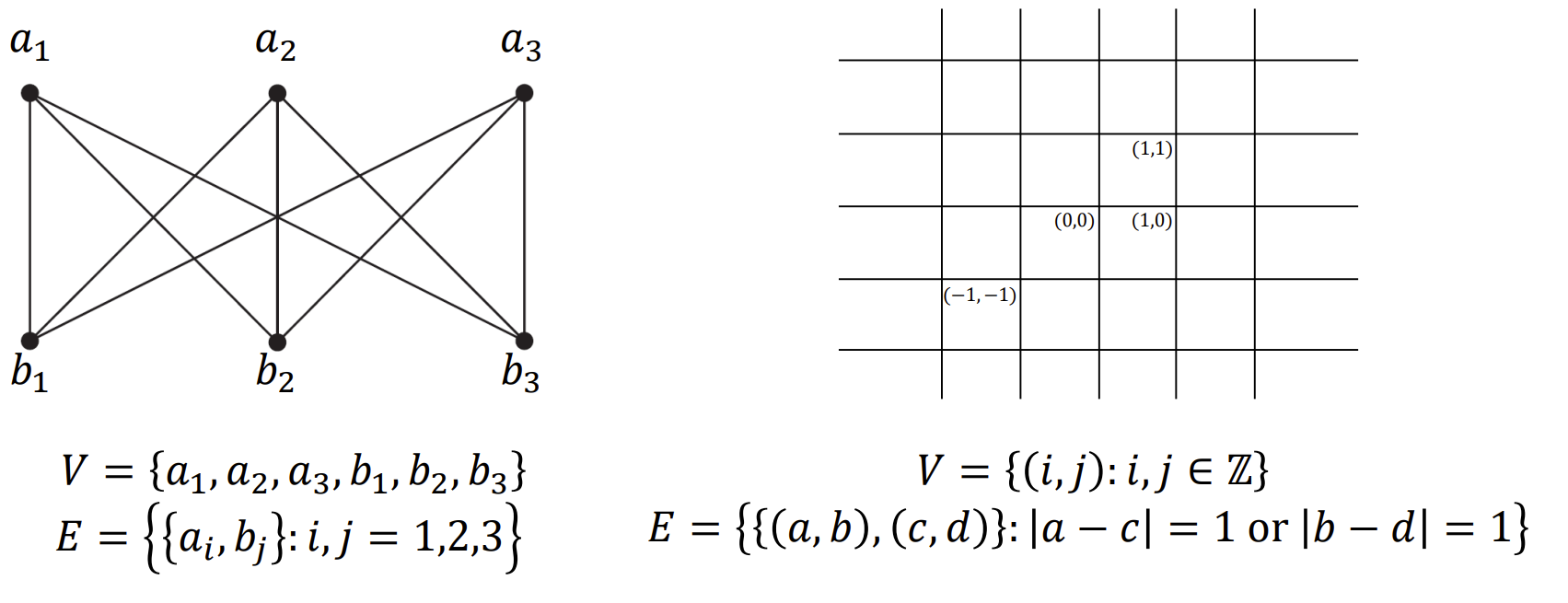
• 循环图/多边图 - Loop& multiple-edge Graph: 循环图: 一个边的端点是同一个顶点, 即$1\to 1$; 多边图: 两个顶点之间有多条直接连接的边

• 简单图 - Simple Graph: 既不循环也没有多边的图

• 加权图 - Weighted Graph: 每条边上有正整数作为权重的图

• 有向图 - directed graph

• 子图 - subgraph

Types of Graphs - 图的分类

• 定义: 令G=(V,E) 是一个图, 顶点集为 $V=\{v_1,v_2,\cdots \}$
  • 边有方向?
    • 有: 有向图 - directed graph
    • 无: 无向图 - undirected graph
  • 多重边?
    • 有: 多重图 - multigraph
    • 无: 简单图 - simple graph
  • 循环?
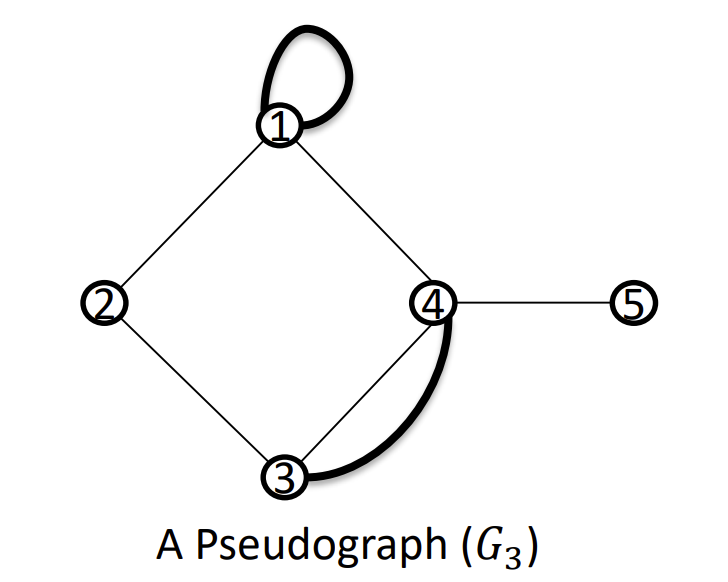
    • 有: 伪图 - pseudograph

Type	Edge	Multiple-edge allowed	Loops allowed
简单图	无向	no	no
多重图	无向	yes	no
伪图	无向	yes	yes
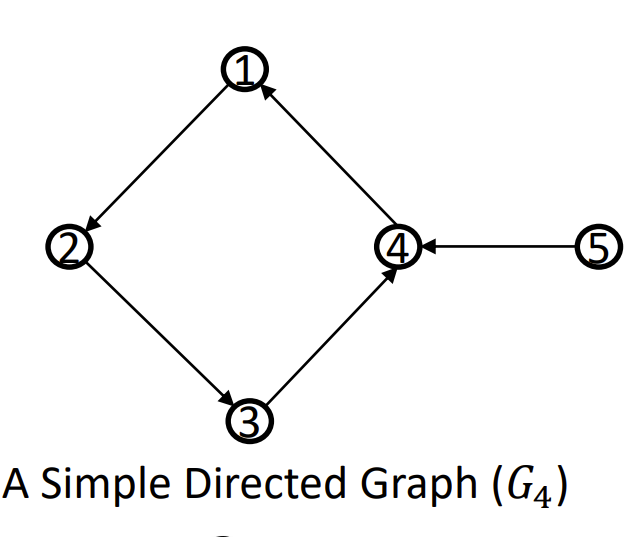
简单有向图	有向	no	no
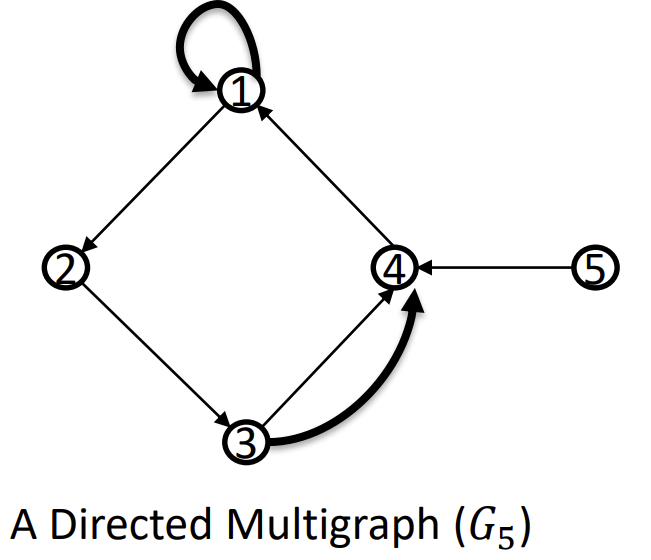
多重有向图	有向	yes	yes
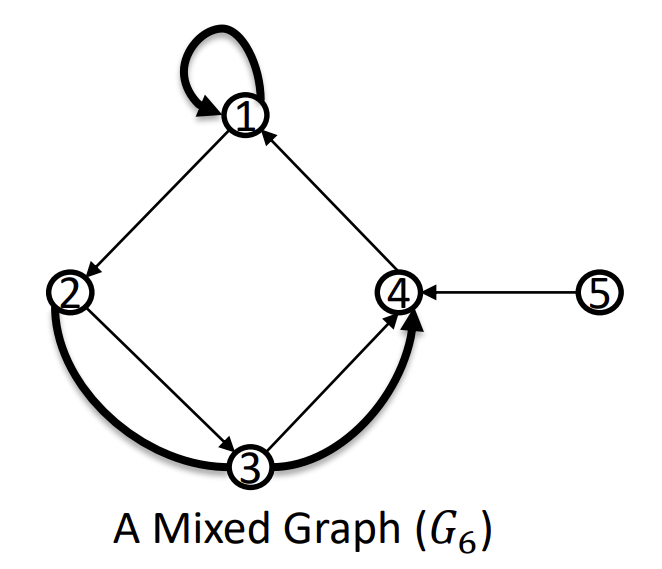
混合图 - Mixed Graph	有向+无向	yes	yes

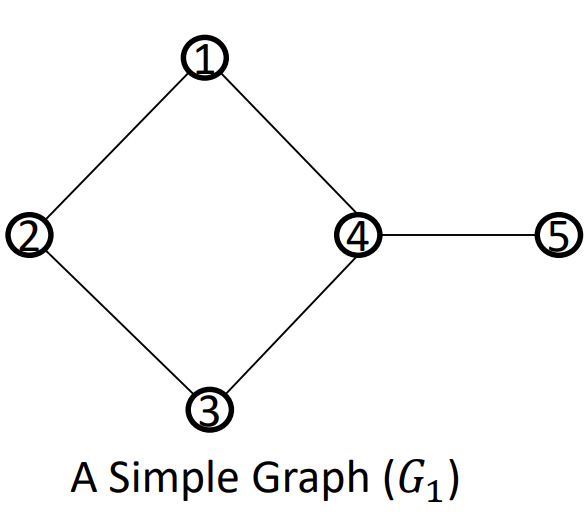
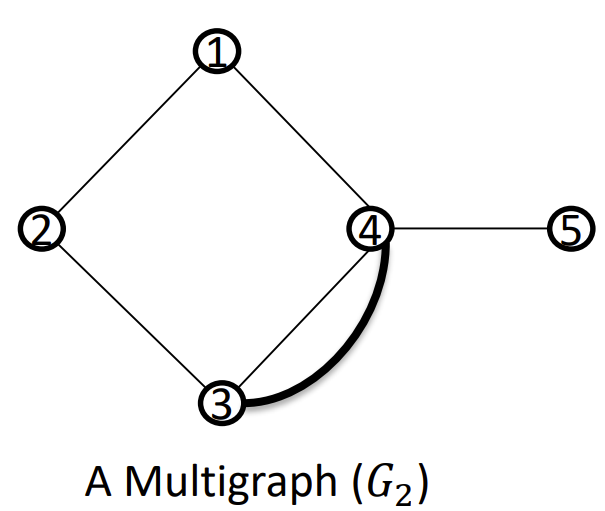
Special Simple Graph - 特殊的简单图

1. 完全图 - Complete Graph: $K_n:V=\{v_1,v_2,\cdots ,v_n\};E=\{(v_i,v_j),1\le i\ne j\le n\}$

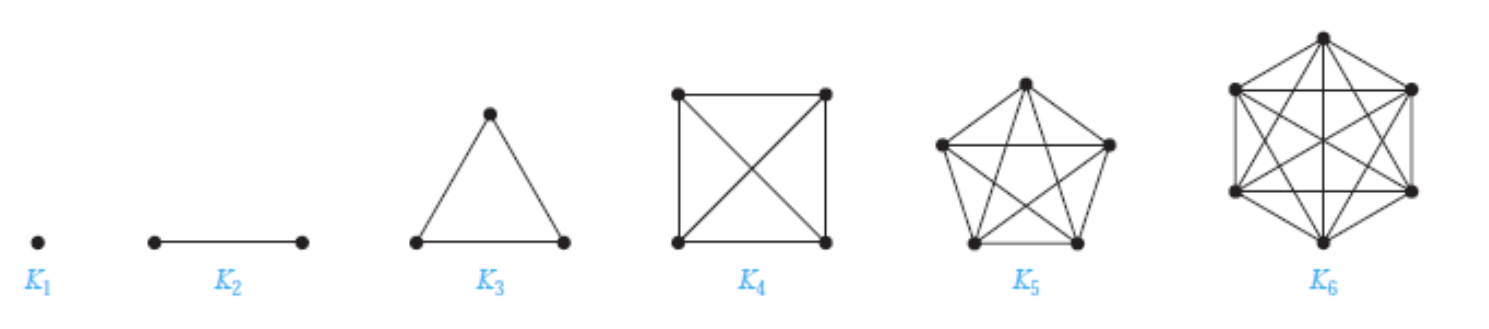
2. 环图 - Circle Graph: $C_n:V=\{v_1,v_2,\cdots ,v_n\};E=\{(v_1,v_2),\cdots .(v_n,v_1)\}$

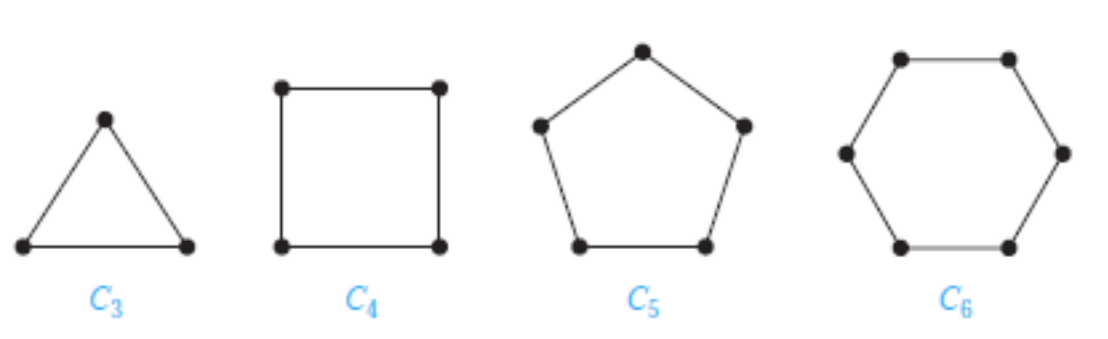
3. 轮图 - Wheel: $W_n:V=\{v_0,v_1,\cdots ,v_n\};E=\{(v_1,v_2),\cdots ,(v_n,v_1)\}\cup \{(v_0,v_1),\cdots ,(v_0,v_n)\}$

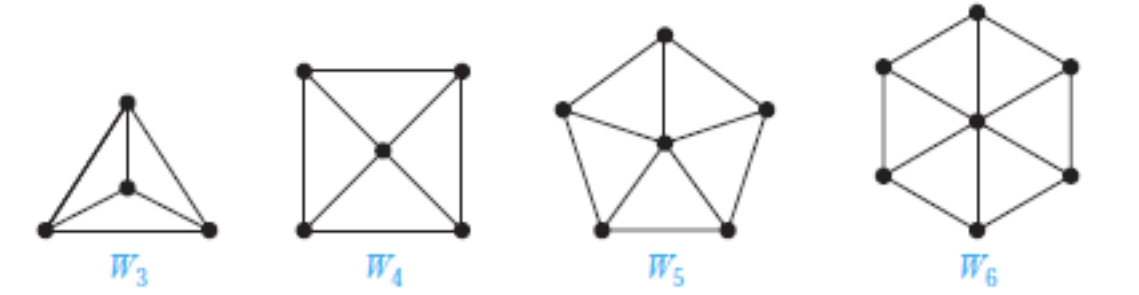
4. 方体 n-Cubes: $Q_n:V\{0,1{\}}^n;E=\{(u,v):d_{(u,v)}=1\},d_{(u,v)}=|\{i\in [n],u_i\ne v_i\}|$

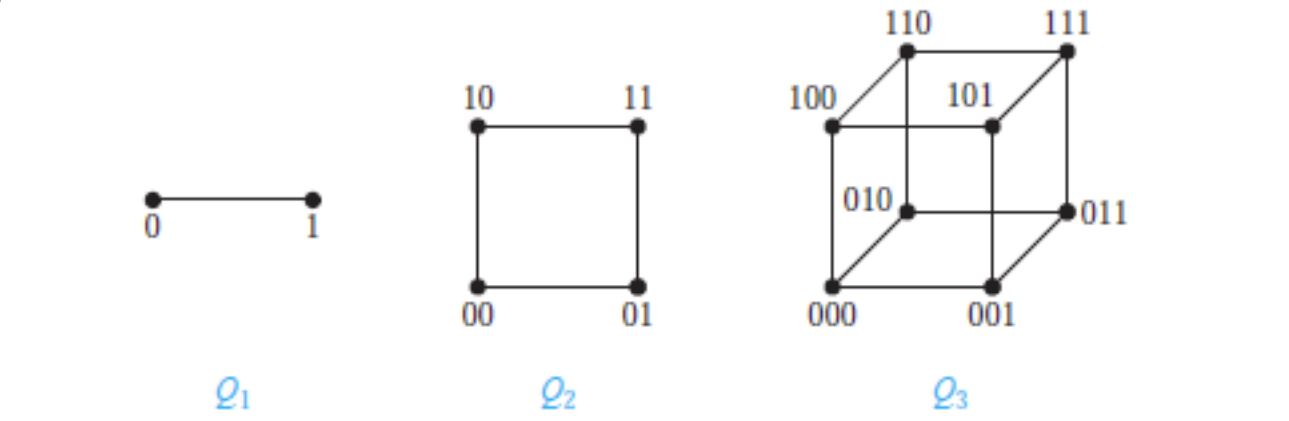
图的表示

Adjacency List - 邻接表

• 定义: 令G=(V,E)是一个没有多边的图, G的邻接表是顶点的列表, 列出所有的相邻顶点
  • 相邻 - adjacent: 如果$v_i,v_j$之间有一条边, 那么他们就是相邻的

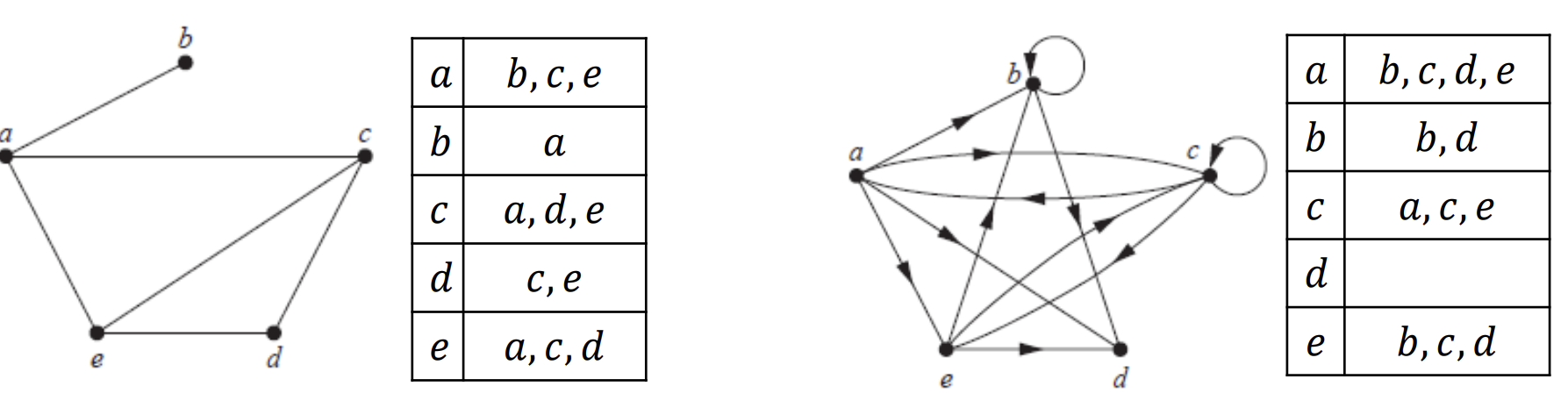
Adjacency Matrix - 邻接矩阵

• 定义: G是一个简单图, 则邻接矩阵是一个$n\times n$的矩阵, $a_{ij}=\{\begin{array}{cc}1& (v_i,v_j)\in E\\ 0& (v_i,v_j)\notin E\end{array}$

Incidence Matrix

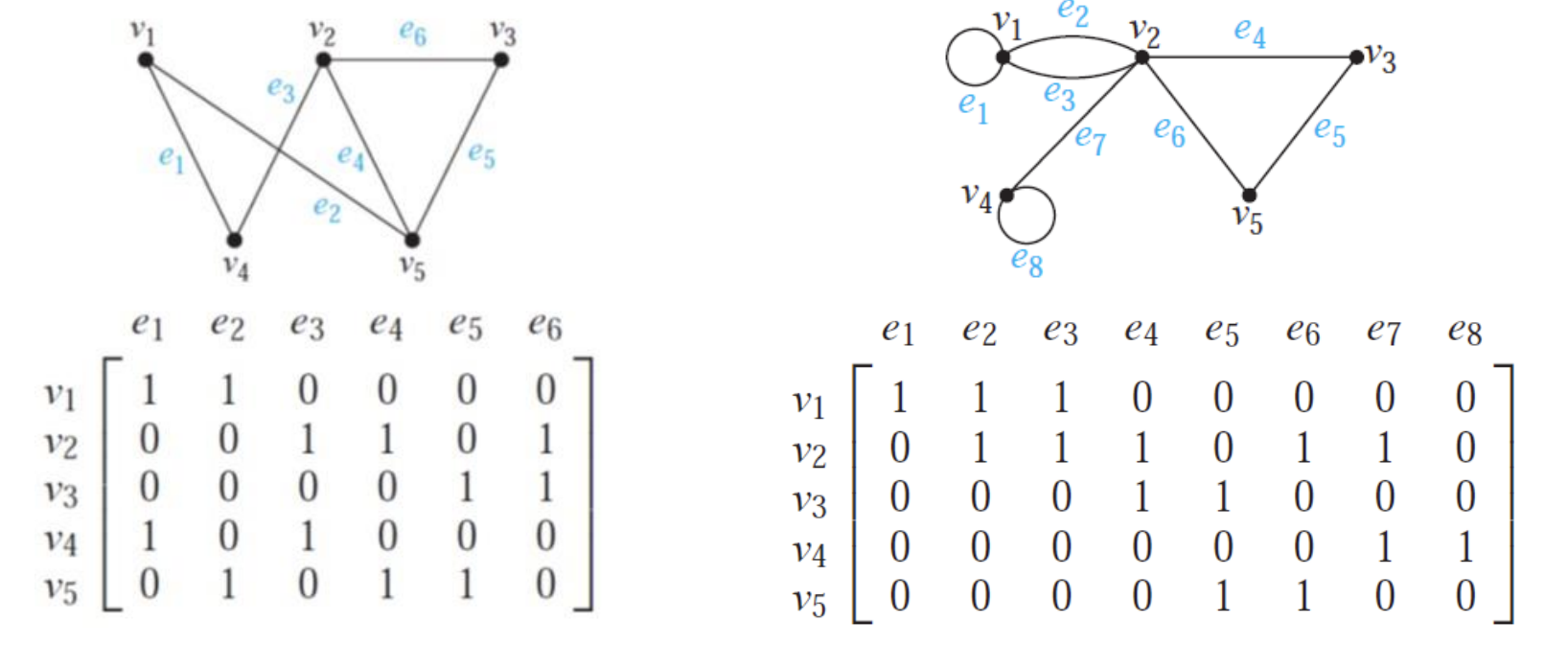
Degree - 度

• 定义: 令 G=(V,E) 是一个无向图, 如果两个顶点之间$(u,v)\in E$, 那么认为u,v是相邻的(adjacent)
  • 邻域 - neighborhood: $N(v)=\{u\in V:(u,v)\in E\};N(A)={\bigcup }_{v\in A}N(v)$ for $A\subseteq V$
  • 度 - degree: $\mathrm{deg}(v)$是与这一点相关联的边的数量
    • 如果$\mathrm{deg}(v)=0$, 那么称点$v$是孤立的(isolated), 如果$\mathrm{deg}(v)=1$, 那么称$v$为悬挂的(pendant)
• 有向图中:
  • (u,v): u是起始点(initial vertex), v是终点(e terminal vertex)
  • 入度 - in-degree
  • 出度 - out-degree

握手定理 - Handshaking Theorem

• 定义: 令G=(V, E)是一个无向图, $2|E|={\sum }_{v\in V}\mathrm{deg}(v)$, and $|\{v\in V:\mathrm{deg}(v)isodd\}|$ is even

• 定义: 令G=(V, E)是一个有向图, 则${\sum }_{v\in V}{\mathrm{deg}}^{-}(v)={\sum }_{v\in V}{\mathrm{deg}}^{+}(v)=|E|$

子图 - Subgraph

• 定义: 令G=(V, E)是一个简单图, H=(W, F), 如果$W\subseteq V,F\subseteq E$, 那么称H为G的子图
  • 真子图 - proper subgraph: H是G的子图且$H\ne G$
  • 导出子图 - subgraph include:
    • $W\subseteq V,F=\{e:e\in E,e\subset W\}$ Notion: $G[W]$
      • 顶点是先去出来(可能会少), 然后把原图G里面这些点相连的边取出来, 连接成H
    • $F\subseteq E,W=\{v:v\in V,v\in eforsomee\in F\}$ Notion: $G[F]$
      • 先取出想要的边, 然后把用到的顶点取出来

减边 - Removing An Edge

• 定义: 令图G=(V, E)是一个简单图, 且边$e\in E$, 则$G-e=(V,E-\{e\})$

加边 - Adding An Edge

• 定义: 简单图G=(V, E), $e\notin E$, 则$G+e=(V,E\cup e)$

缩边 - Edge Contraction

• 定义: 简单图G=(V, E), $e=\{u,v\},G/e=(V^{\prime },E^{\prime })$, $V^{\prime }=(V-\{u,v\})\cup \{w\}$, $E^{\prime }=\{e^{\prime }\in E:e^{\prime }\cap e=\varnothing \}\cup \{\{w,x\}:\{u,x\}\in Eor\{v,x\}\in E\}$

就是把两点之间的边缩成了一个点, 两个点上的所有相连边都合在了所完之后的点上

减点 - Removing Vertex

• 定义: $G-v=(V-v,E^{\prime }),E^{\prime }$是剪完顶点之后还能存在的边

补图 - Complement

• 定义: 简单图G=(V, E), 阶数是n, 定义补图为G’=(V, E’), $E^{\prime }=\{\{u,v\}:u,v\in V,u\ne v,\{u,v\}\notin E\}$

图的同构 - Graph Isomorphism

• 定义: 如果有双射$\sigma :V_1\to V_2$, 有$\{u,v\}\in E_1\iff \{\sigma (u),\sigma (v)\}\in E_2$, 则称图$G_1=(V_1,E_1),G_2=(V_2,E_2)$是同构的
  • $\sigma$被称为同构映射(isomorphism)

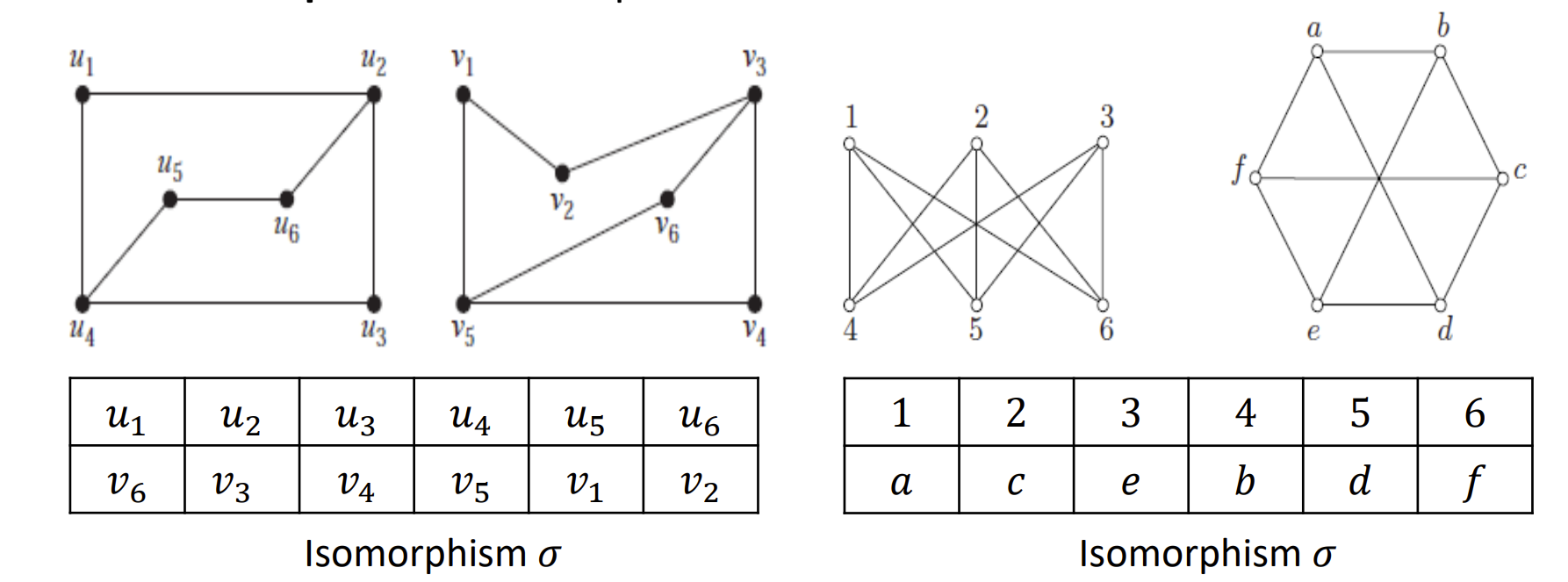
图的常项 - Graph Invariants

• 定义: 同构的图中不会改变的属性

如:

• 顶点个数
• 边的个数
• 某个度的顶点个个数
• 后面还有[路径](#路径和同构 - Path and Isonorphism)

二分图 - Bipartite Graph

• 定义: 如果$V$有一个划分$\{V_1,V_2\}$, 满足$E\subseteq \{\{u,v\}:u\in V_1,v\in V_2\}$, 则称图G=(V, E)是一个二分图

就是把上面分成一个集合,下面分成一个集合, 只有上面与下面相连(两个集合之间相连), 但集合与集合之间不相连

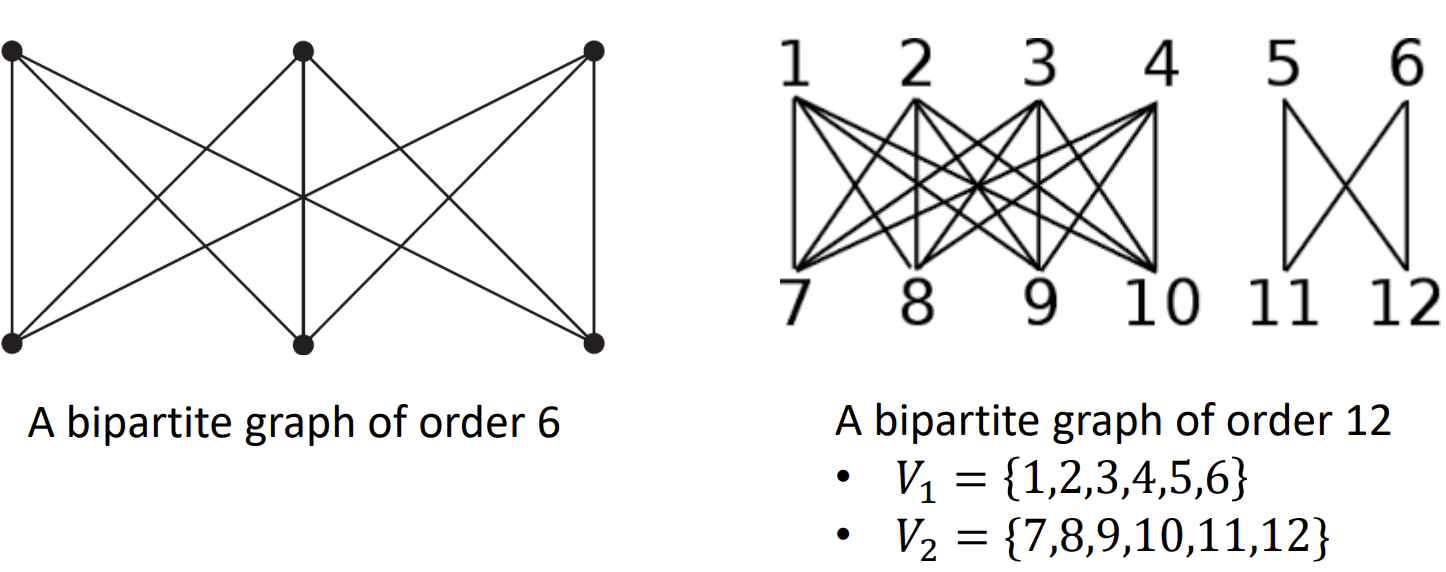
完全二分图 - Complete Bipartite Graph

• 定义: $K_{m,n}=(V,E),V=\{x_1,x_2,\cdots ,x_m\}\cup \{y_1,y_2,\cdots ,y_n\},E=\{\{x_i,y_j\}:i\in [m],j\in [n]\}$

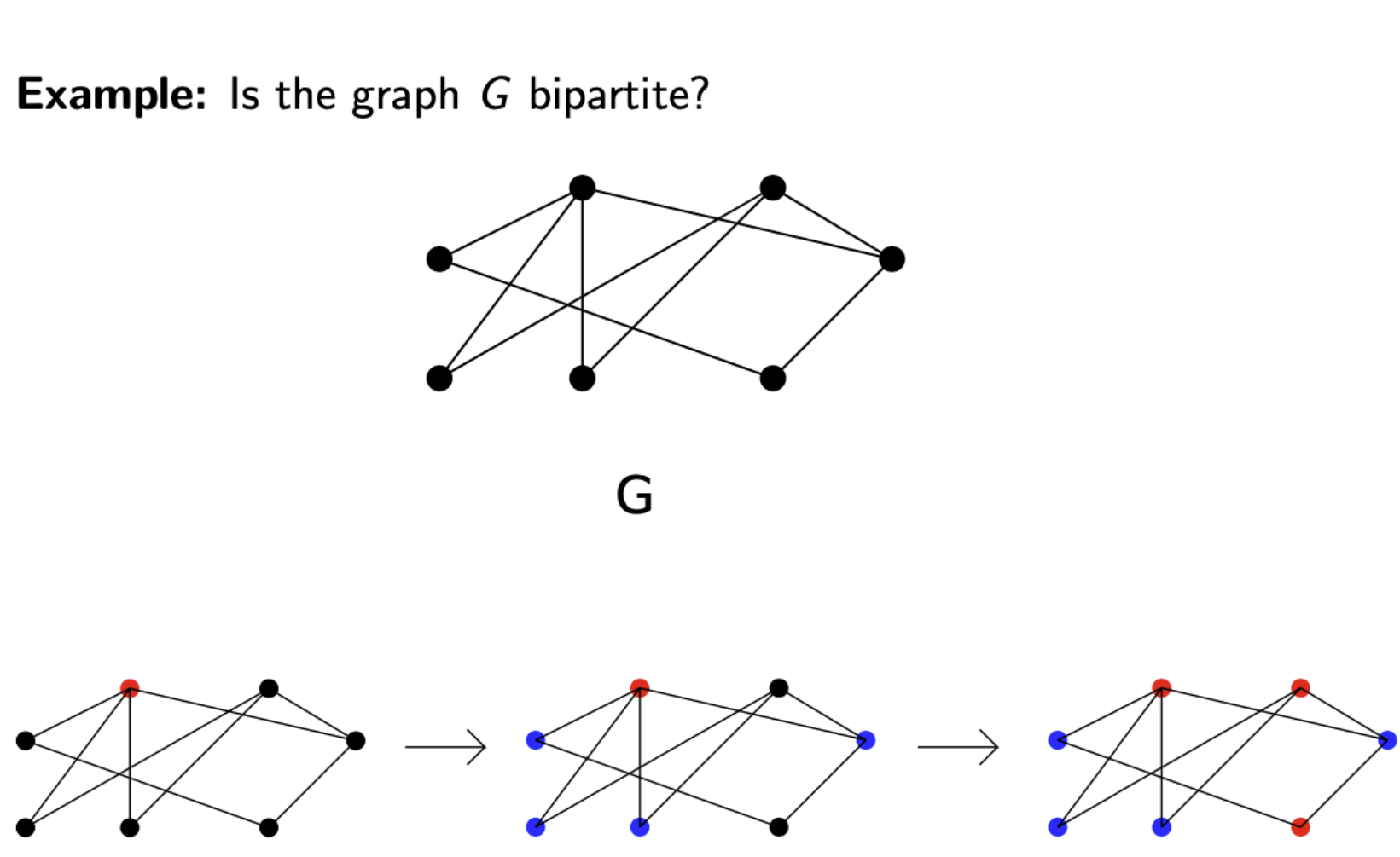
判断是否是二分图

• 首先是简单图
• 将一个顶点染上一种颜色(eg. 红色)
• 与这个顶点相连的点都染上另一种颜色(eg. 蓝色)
• 然后再把与蓝色相连的点染上红色, 如此重复, 直到所有顶点都染上色
• 如果有一个点既是蓝色又是红色, 那么不是二分图
• 如果一条边有相同颜色的顶点相连接, 那么就不是二分图, 否则是二分图

数学版本:

• 如果有映射$f:V\to \{1,2\},f:v\mapsto \{\begin{array}{cc}1& v\in V_1\\ 2& v\in V_2\end{array}$, 满足$\{x,y\}\in E\Rightarrow f(x)\ne f(y)$

匹配 - Matching

• 定义: 边的子集, 使得边之间不相交(没有共享的节点).
  • 最大匹配 - maximum matching: 一个有最大数量边的匹配
  • 完全匹配 - complete matching: $V_1$到$V_2$中$V_1$的每一个点都被匹配到.

Hall’s Theorem

• 定义: 一个二分图$G=(X\cup Y,E)$当且仅当$|N(A)|\ge |A|$对任意的$A\subseteq X$时, 有一个完全匹配

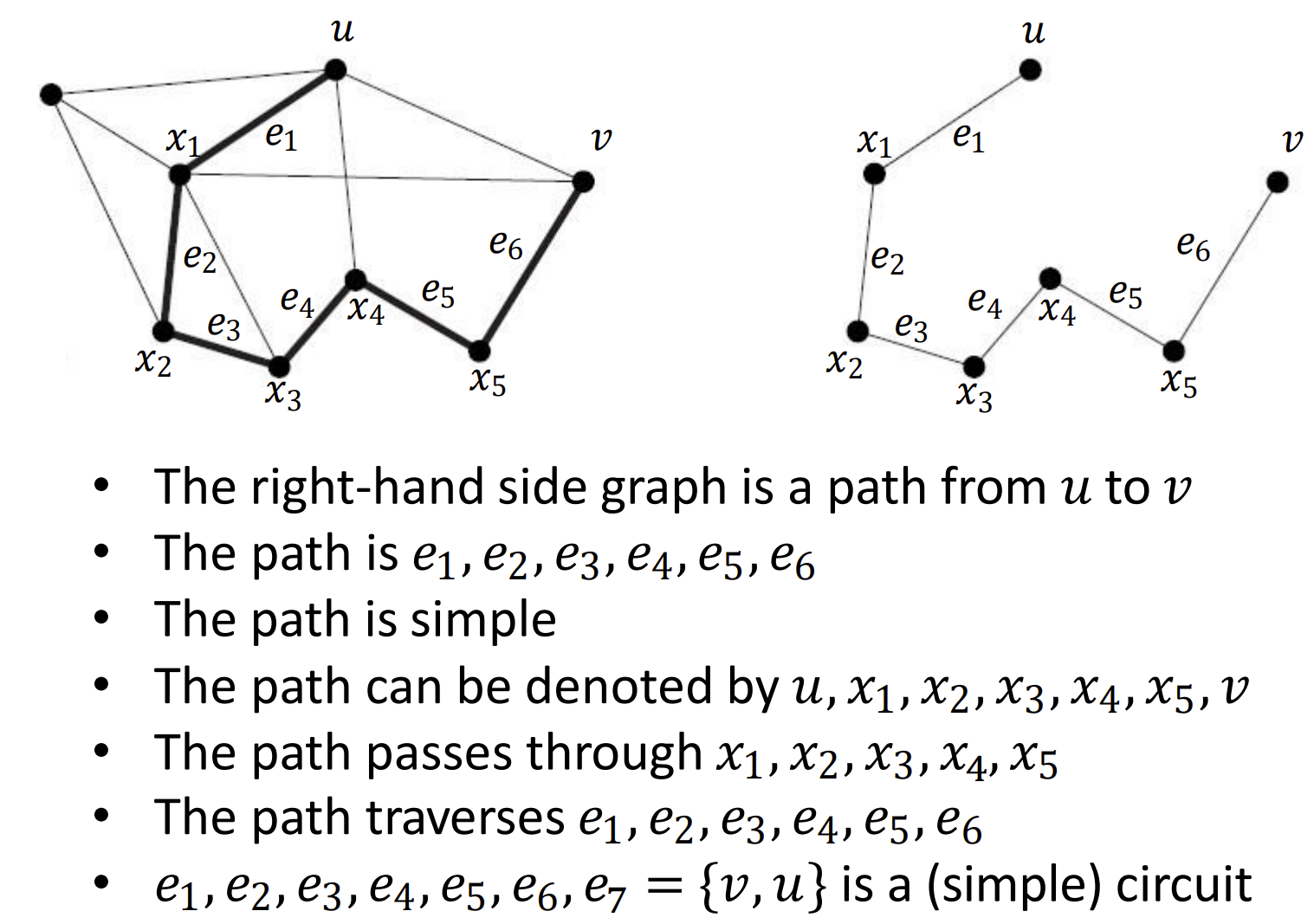
路径 - Path

• 定义: 令图$G=(V,E)$是一个无向图, 令$k\in \mathbb{N}$. 从图$G$中的一点$u$到一点$v$的长度为$k$的路径为一个$k$边的序列$\{e_1,e_2,\cdots ,e_k\}$, 经过顶点$x_0=u,x_1,x_2,x_3,\cdots ,x_{k-1},x_k=v$, 其中$e_i=(x_{i-1},x_i),\forall i\in [k]$
  • 如果$u=v$且$k>0$, 那么成这个路径为回路(circuit)
  • 这个路径经过(pass through)顶点$x_0,x_1,x_2,\cdots ,x_k$
  • 这个路径遍历(traverse)边$e_1,e_2,\cdots ,e_k$
  • 这个路径是简单的(simple)当路径不包含重复的边
  • 如果路径是简单的, 那么可以被写成$x_0,x_1,\cdots ,x_k$的形式

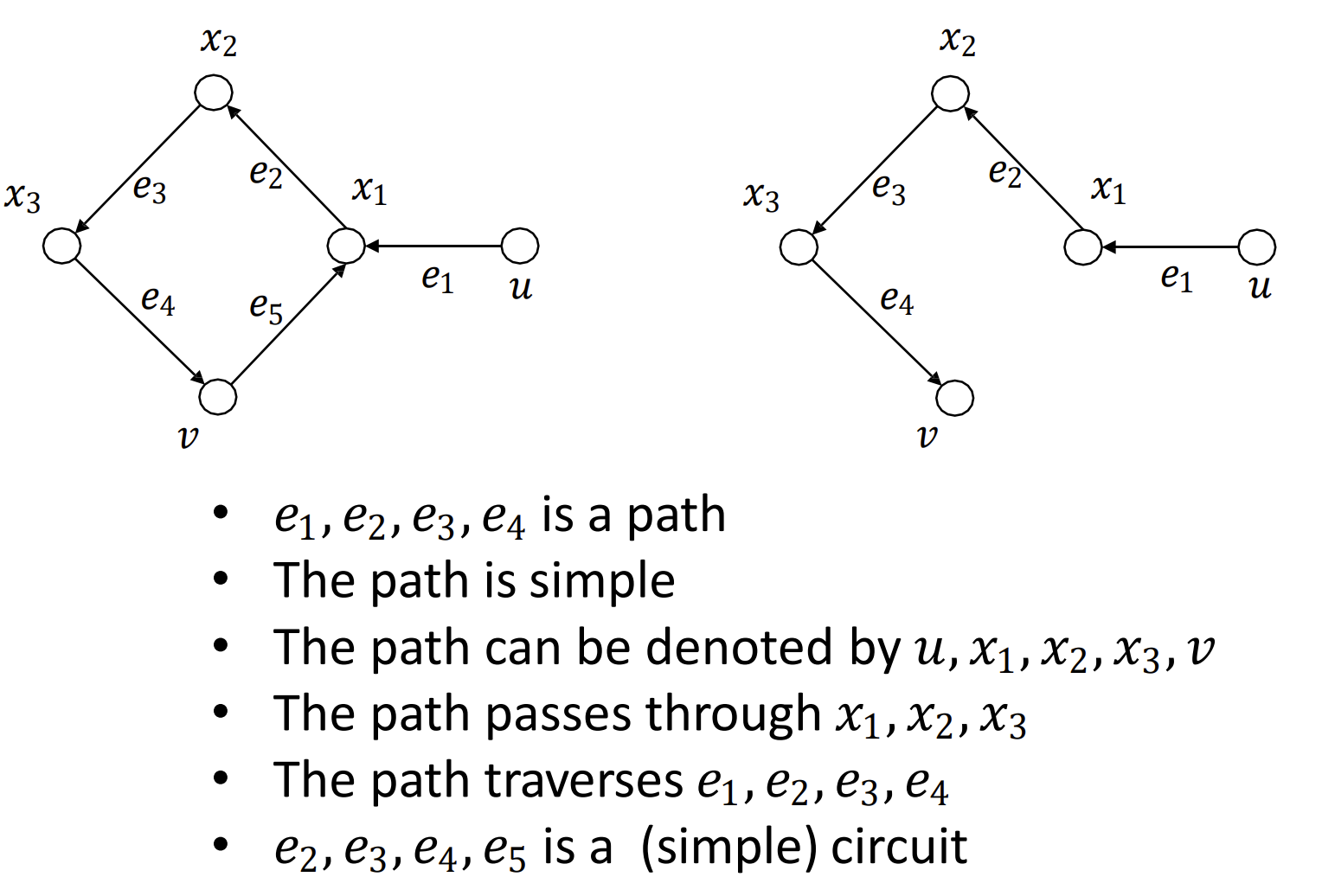
• 有向图也是一样的定义, 但是注意, 有向图的边的顺序是固定的, 有前面的顶点指向后面的顶点.

连通 - connectivity

• 定义: 对于任意一对顶点, 如果有一条路径连接这两个点, 那么这个图是连通的
• 定理: 令图$G$是一个连通的无向图, 那么任意一对顶点之间是有一条简单路径的.

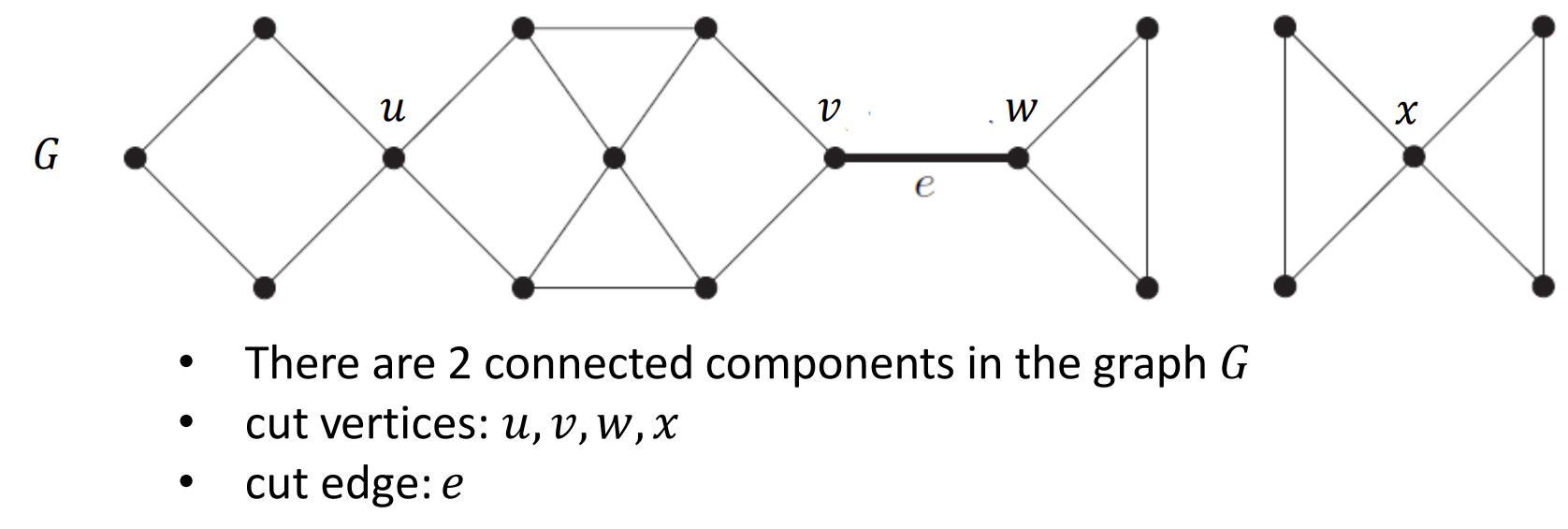
连通分支 - connected component

• 定义: 一个连通分支图中的连通子图, 而且必须是一个非真子图, 或者说, 是一个最大连通子图,

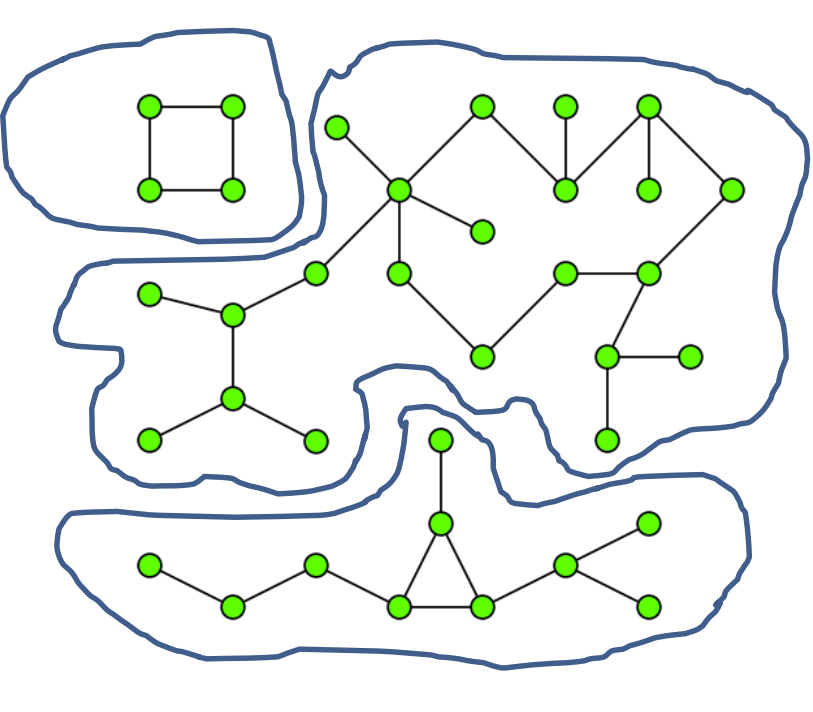
• 切点 - cut vertex: 去掉这个点会有更多的连通分支产生
• 切边 - cut edge: 去掉这个边会有更多的连通分量产生

点连通度 - Vertex Connectivity

• 不可分的 - nonseparable: 如果一个图没有切点, 那么就是不可分的
• 点割集 - vertex cut: $V^{\prime }\subseteq V$, 且满足$G-V^{\prime }$是不连通的, 那么$V^{\prime }$是一个点割集
• 点连通度 - vertex Connectivity: $\kappa (G)$: 使图$G$不连通需要移除的最少节点数
  • 如果$G$不连通, 那么$\kappa (G)=0$
  • 如果$G$是一个完全图$K_n$, 那么$\kappa (G)=n-1$
  • 否则, $\kappa (G)$是点割集中的元素的数量

• 定理: 如果$G=(V,E)$是一个简单图, 阶为n, 那么

  • $0\le \kappa (G)\le n-1$
  • $\kappa (G)=0$ iff $G$ 是不连通的或者$G=K_1$
  • $\kappa (G)=n-1$ iff $G=K_n$

• k-连通 - k-connectivity: $\kappa (G)\ge k$

  • $G$是1-连通的 当且仅当 $G$是连通的且$G\ne K_1$
  • $G$是2-连通的 当且仅当 $G$是不可分割的且阶数大于等于3
  • $G$是$k$连通的 当且仅当 $G$是$j$连通的对于$\forall j\in \{0,1,\cdots ,k\}$

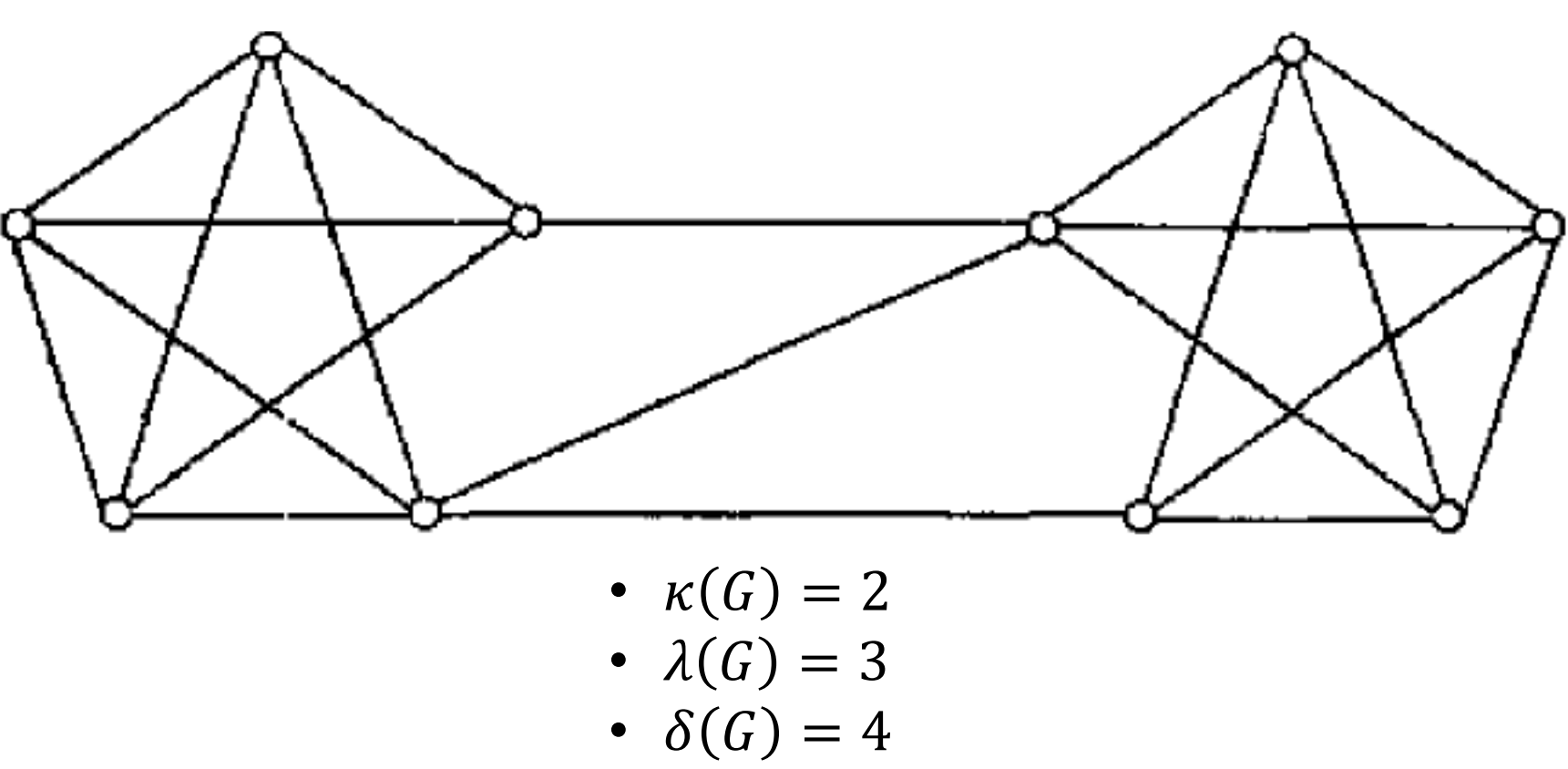
边连通度 - edge connectivity

• 边割集 - edge cut: 使得简单连通图$G$变成不连通的需要删掉的边
• 边连通度 - edge connectivity: $\lambda (G)$: 如果$G$是不连通的, $\lambda (G)=0$. 如果$|V|=1$, 那么$\lambda (G)=0$. 如果$|V|\ge 1$, 那么$\lambda (G)$是最小边割集中的元素的个数

连通度 - connectivity

• 定理: 简单图$G$, $\kappa (G)\le \lambda (G)\le \delta (G)$, $\delta (G)={\min }_{v\in V}\mathrm{deg}(v)$

有向连通图 - connected directed graph

• 强连通-定义: 如果图$G=(V,E)$是一个有向图, 如果对于任意$u,v\in V$, 有从$u\to v$和从$v\to u$的路径, 那么就是强连通的.
• 弱连通-定义: 如果去掉边的方向后图是连通的

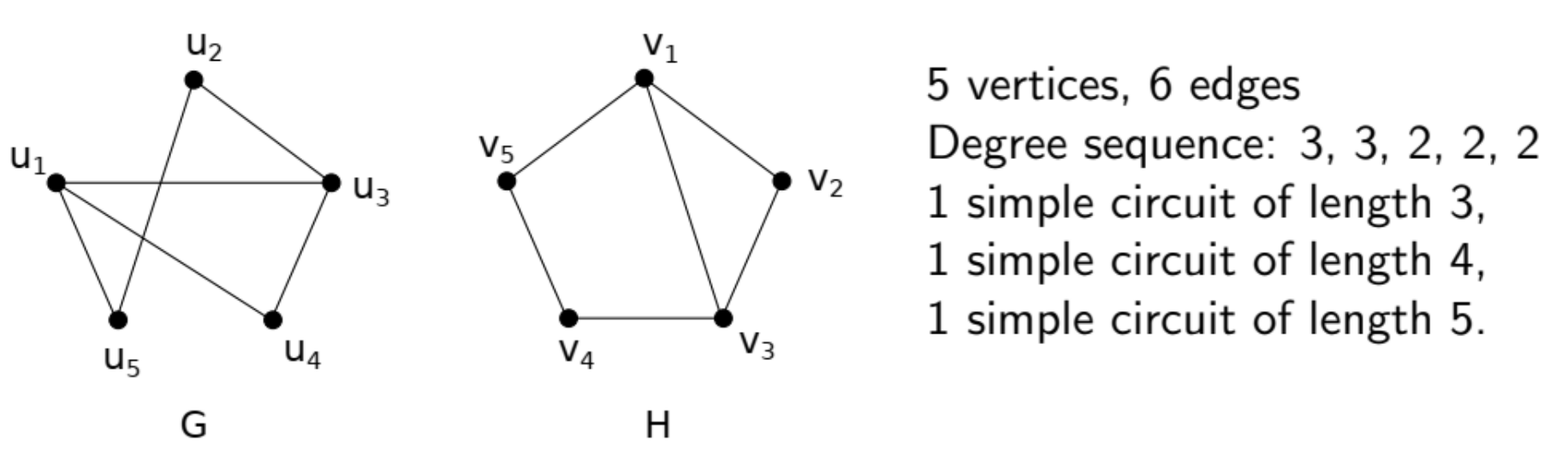
路径和同构 - Path and Isonorphism

• 定理: 如果有一个简单回路,长度为$k$, 如果$k>3$, 那么这个回路也是简单图的常项

• 其他的图的常项: [常项](#图的同构 - Graph Isomorphism)

路的计数 - Counting Paths Between Vertices

• 定义: $G$是一个图, 邻接矩阵是$A$, 判断$(i,j),i,j\in V$之间有多少长度是$r$的路径, 只需要看$A^r$中$(i,j)$点的值是多少即可

欧拉七桥问题

• 定义: 令图$G=(V,E)$, 边只遍历一次

  • 欧拉路径 - Euler Path: 简单路径遍历所有顶点
  • 欧拉环路 - Euler Circuit: 简单环路遍历所有的顶点

• 定义: 令图$G=(V,E)$是一个阶数为2的连通多重图, 当且仅当$2\mid \mathrm{deg}(v),\forall v\in V$时图$G$有欧拉回路

• 无向图:

  • 如果所有的点的度都是偶数, 那么存在欧拉回路
  • 如果奇数度的点只有2个, 那么存在欧拉通路(路径)

• 有向图:

  • 所有点的入度等于出度, 那么存在欧拉回路
  • 可以允许有且仅有两个点的入度不等于出度, 或者所有点入度出度都相等, 那么有欧拉通路

• 欧拉图: 有欧拉回路

• 半欧拉图: 有欧拉通路

Hierholzer算法

1. 在一个欧拉图中, 以任意一个顶点为起点, 遍历与之相邻的顶点
2. 深搜, 访问相邻的节点, 将经过的边删除
3. 如果当前顶点没有相邻边, 那么把这个点入栈
4. 倒序输出栈中的顶点, 即为一个欧拉回路

哈密顿路径 - Hamilton Path

• 定义: 只遍历一次顶点的路径

• 哈密顿环:只遍历一次顶点的环路

• 但是判断是否有哈密顿环还是一个NP-Complete问题

• 必要条件: 有一个度为1的顶点那么不能有哈密顿环; 有一个度为2的顶点那么哈密顿环遍历所有的边

• 充分条件:

  令$G=(V,E)$是一个简单图,阶数$n\ge 3$,

  • Ore’s定理: 如果$\mathrm{deg}(u)+\mathrm{deg}(v)\ge n,\forall \{u,v\}\notin E$, 那么G有哈密顿环
  • Dirac’s定理: 如果$\mathrm{deg}(u)\ge \frac{n}{2},\forall u\in V$, 则G有哈密顿环

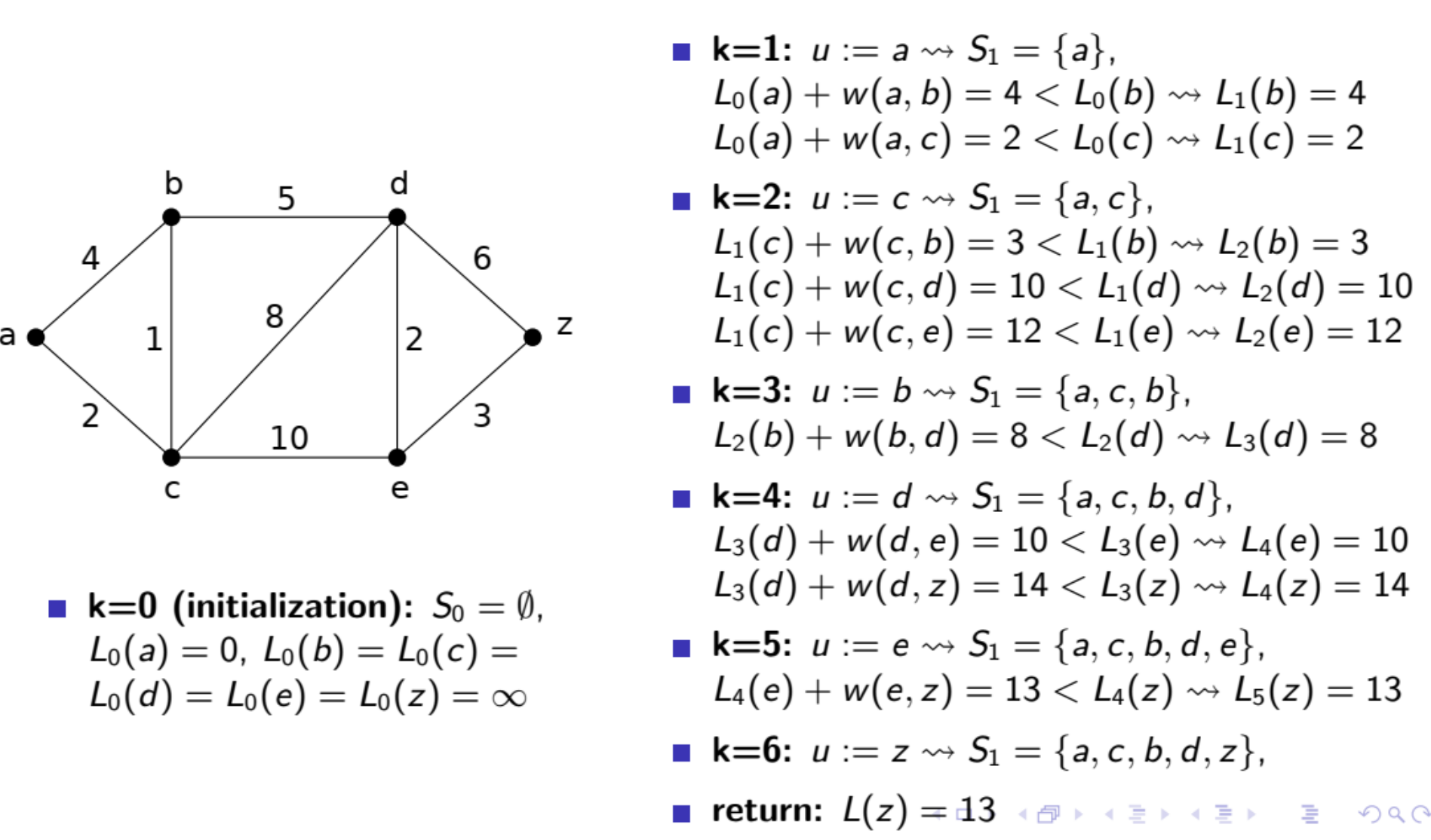
最短路问题 - Shortest Path Problem

每个边都有权重, 找到两点之间权重之和最小的一条路径

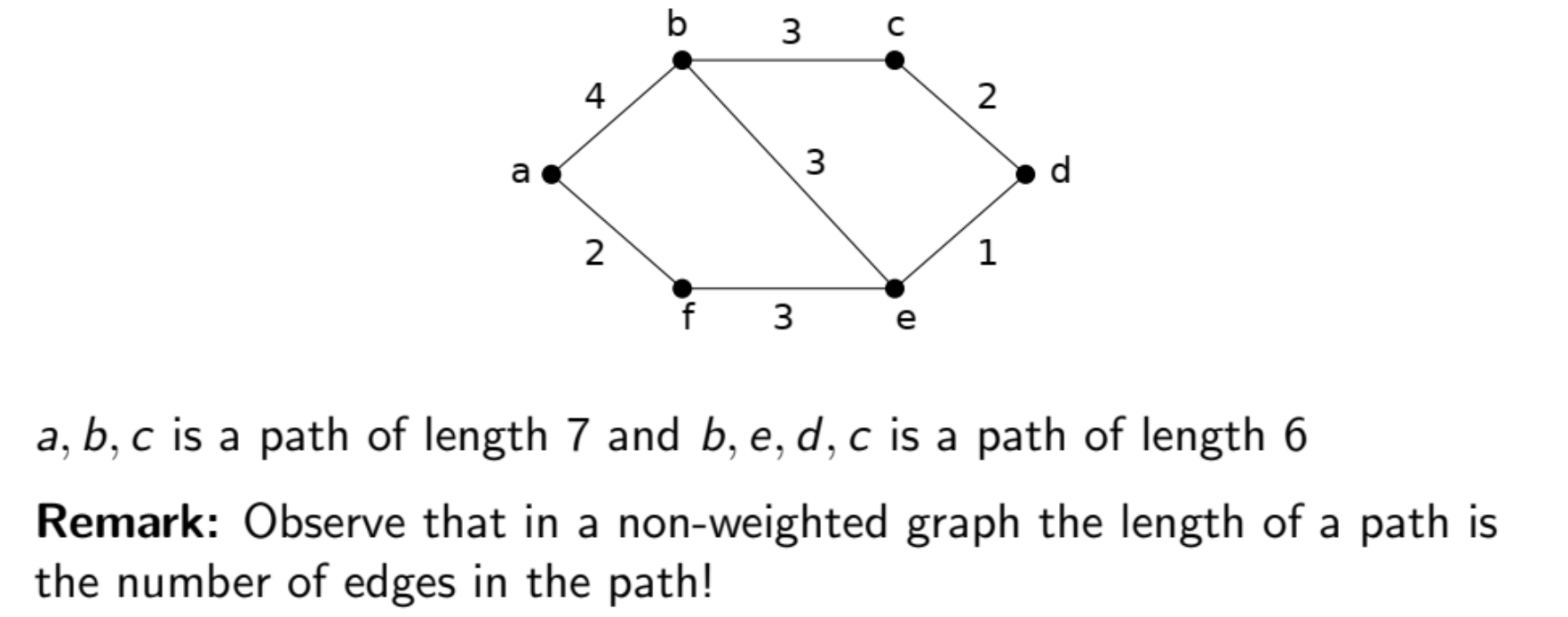
问题: 找到ad之间最短路径

方法: 找到距离a最近的顶点, 再找第二近的, …, 直到找到d $\Rightarrow$ Dijkstra’s Algorithm

Dijkstra算法

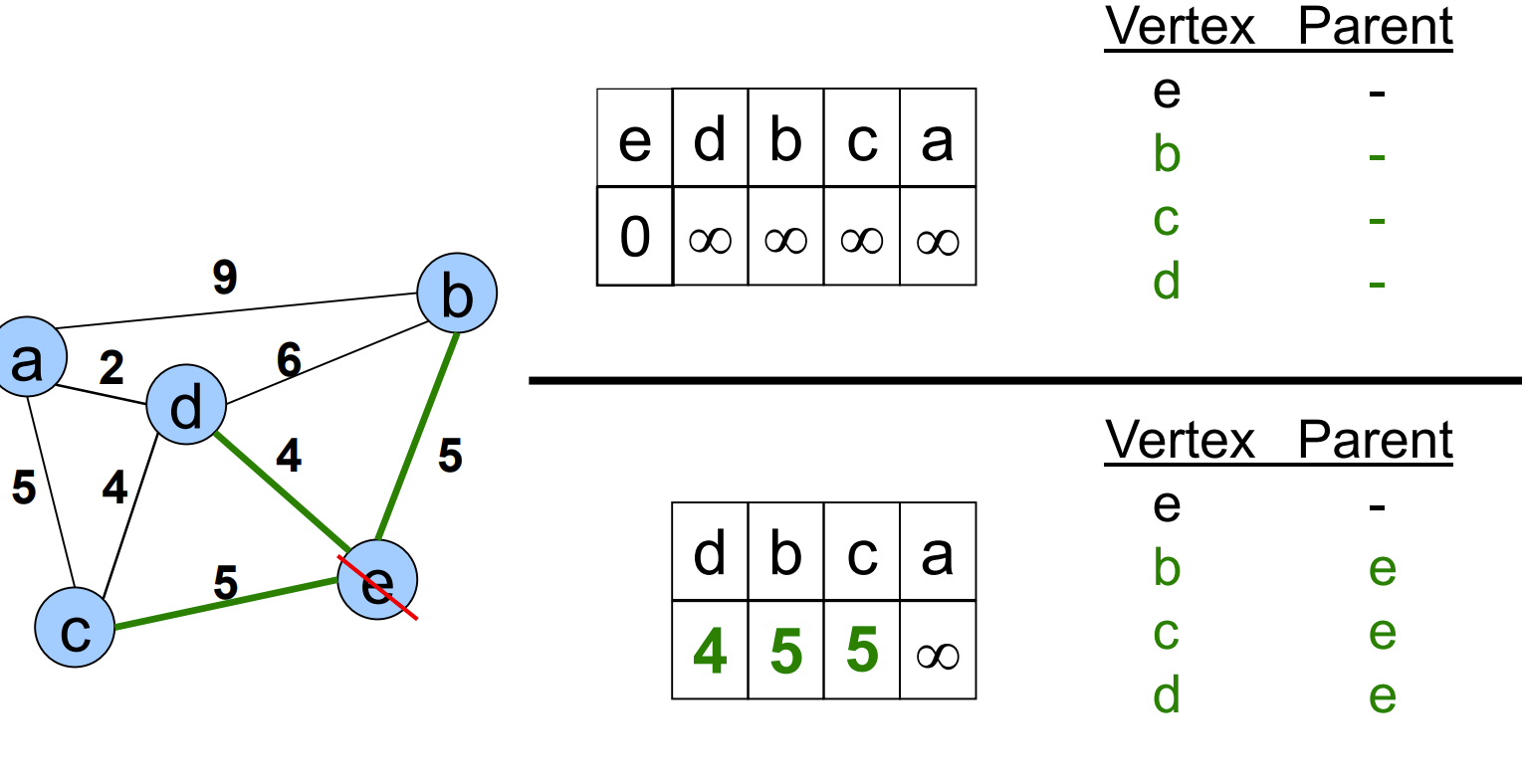
1. 找a到任意相连的路径的最短路:

   {a,b}=4,{a,f}=2: 最近的点是f

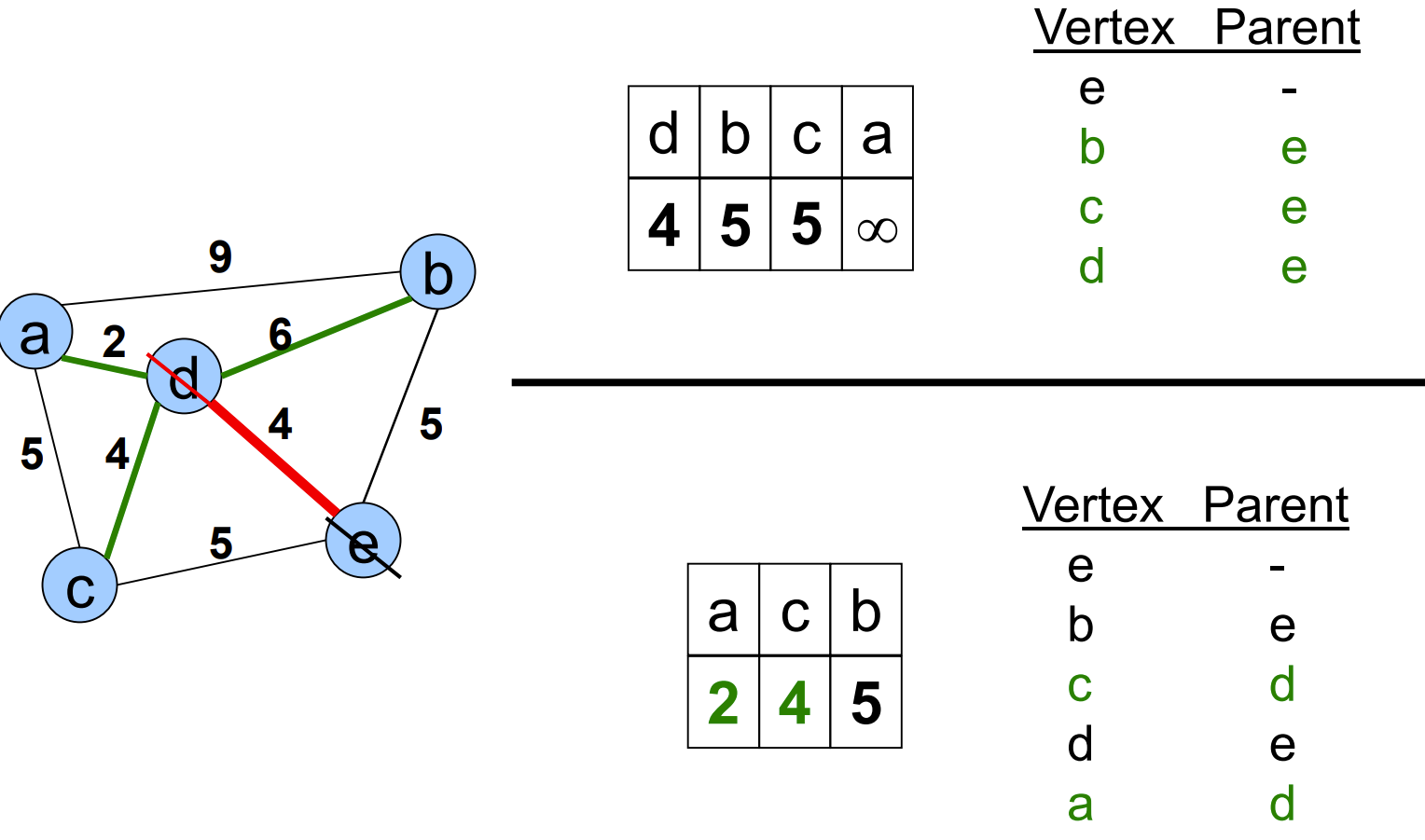
2. 现在已经有点集{a,f}, 和剩余的点集{b,c,d,e}, 然后通过边来找到距离a第二近的点.

   从a出发: {a,b}=4; 从f出发: {a,f,e}=5

   所以第二近的点是b

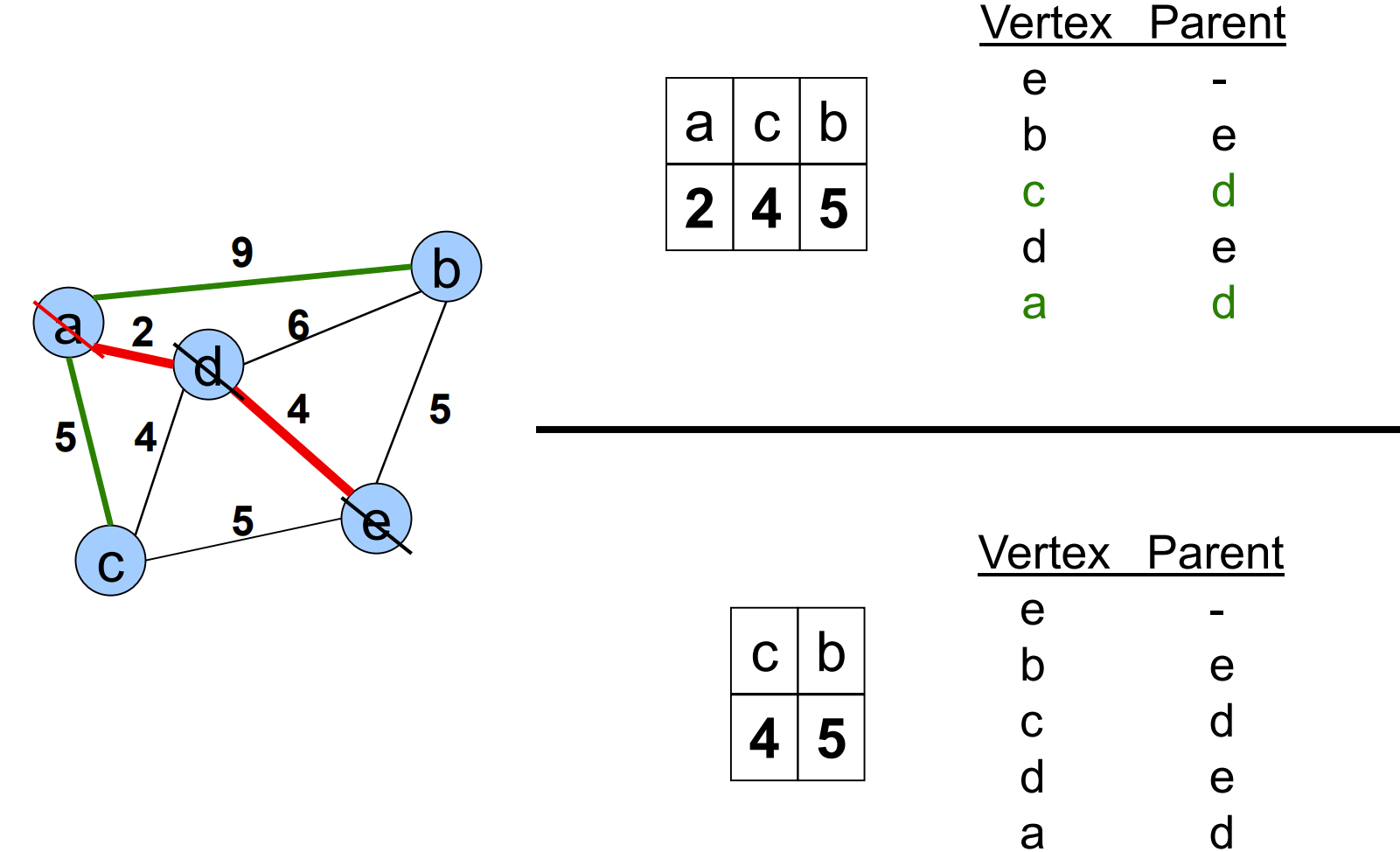
3. 现在已有点集{a,f,b}, 剩余点集{c,d,e}, 更新第三近的点

   a出发: 全部遍历过; b出发: {a,b,c}=7,{a,b,e}=7; f出发: {a,f,e}=5

   第三近的点是e

4. 已有点击{a,f,b,e}, 剩余点集{c,d},更新第四近的点

   a,f出发: 全部遍历过; b出发: {a,b,c}=7,{a,b,e}=7; e出发: {a,f,e,d}=6(找到d)

5. a到d的最短路是6

$O((N+M)\log (N))$

贪心, 局部最优解去更新下一步的最优, eg. 在e点的dis是用f.dis更新而不是b.dis更新, 因为b.dis>f.dis.

旅行者问题 - Travel Salesperson Problem

从一个城市出发, 经过所有城市一次, 并回到自己的城市, 问, 怎么用最短路径

• 完全图中哈密顿环的最短路径

完全遍历(没有简化算法)

平面图 - Planer Graph

• 定义: 没有交叉边的图是平面图

• e.g.

  • $K_1,K_2,K_3,K_4$
  • $K_{1,n},K_{2,n}$
  • $C_n,W_n,n\ge 3$
  • $Q_1,Q_2,Q_3$

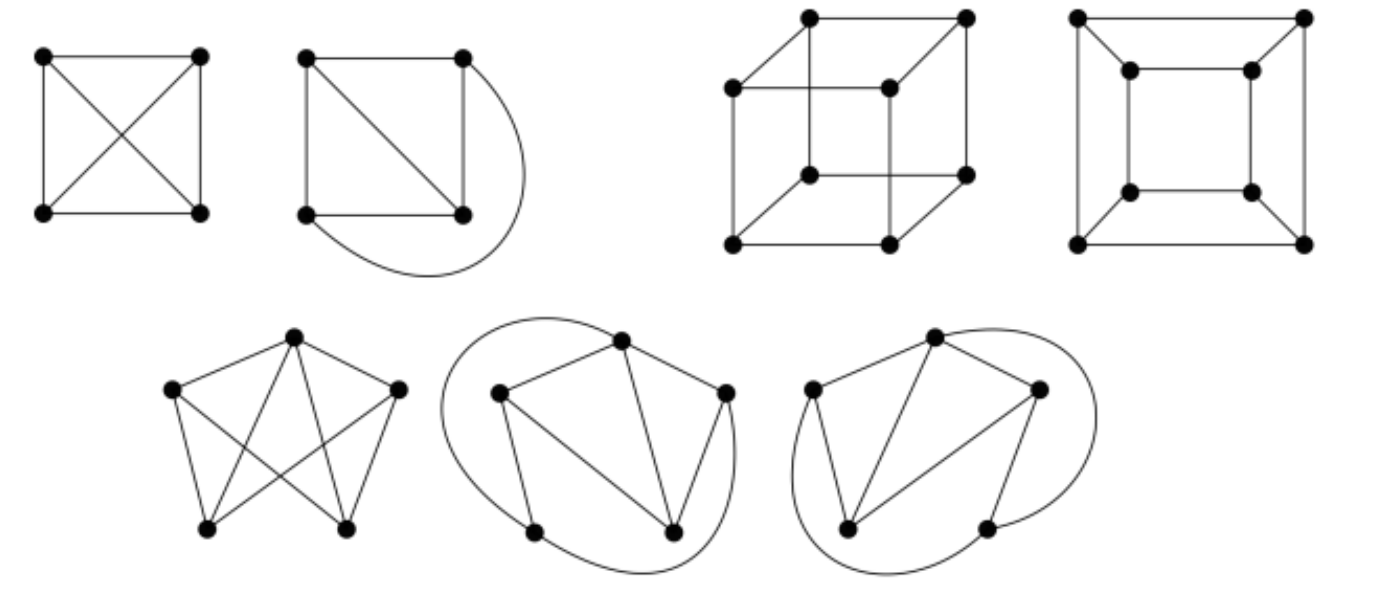
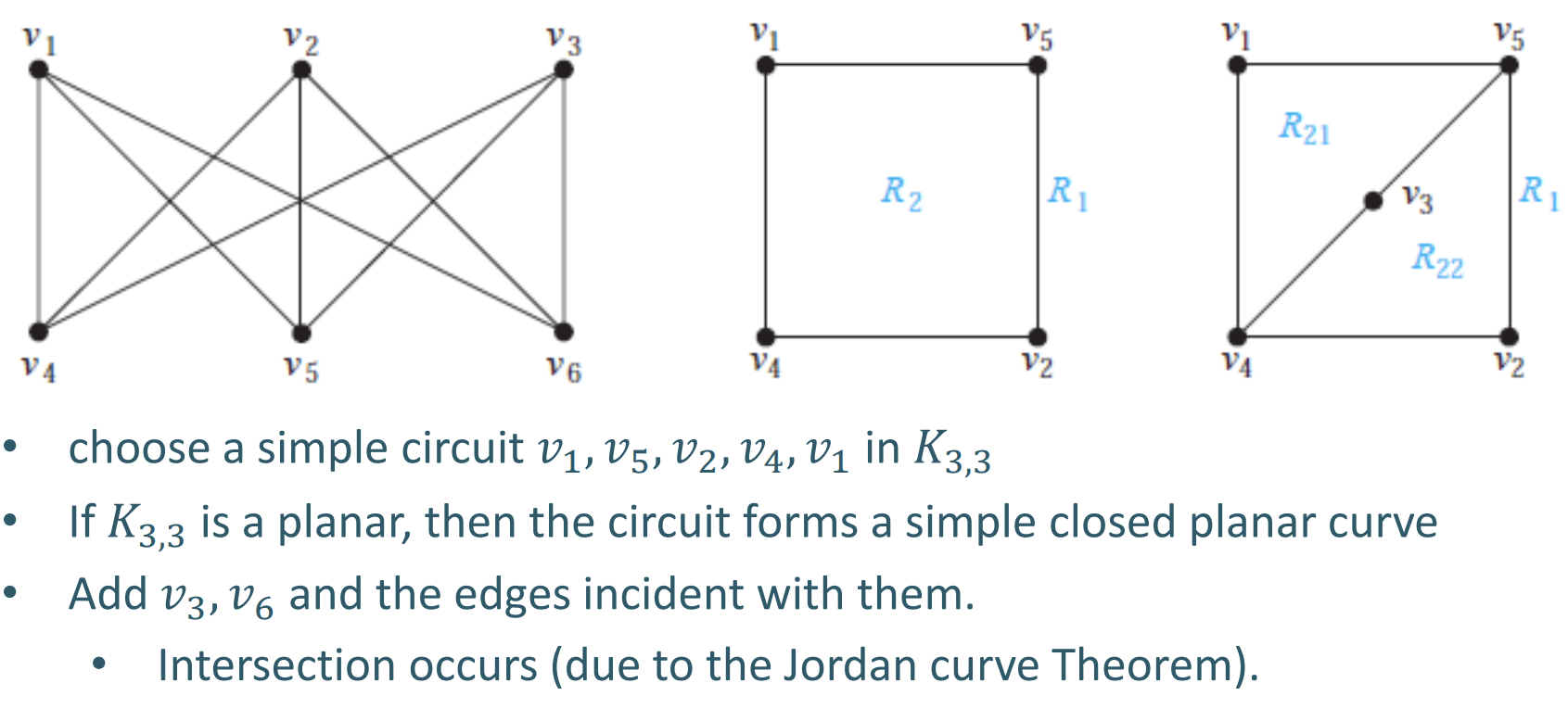
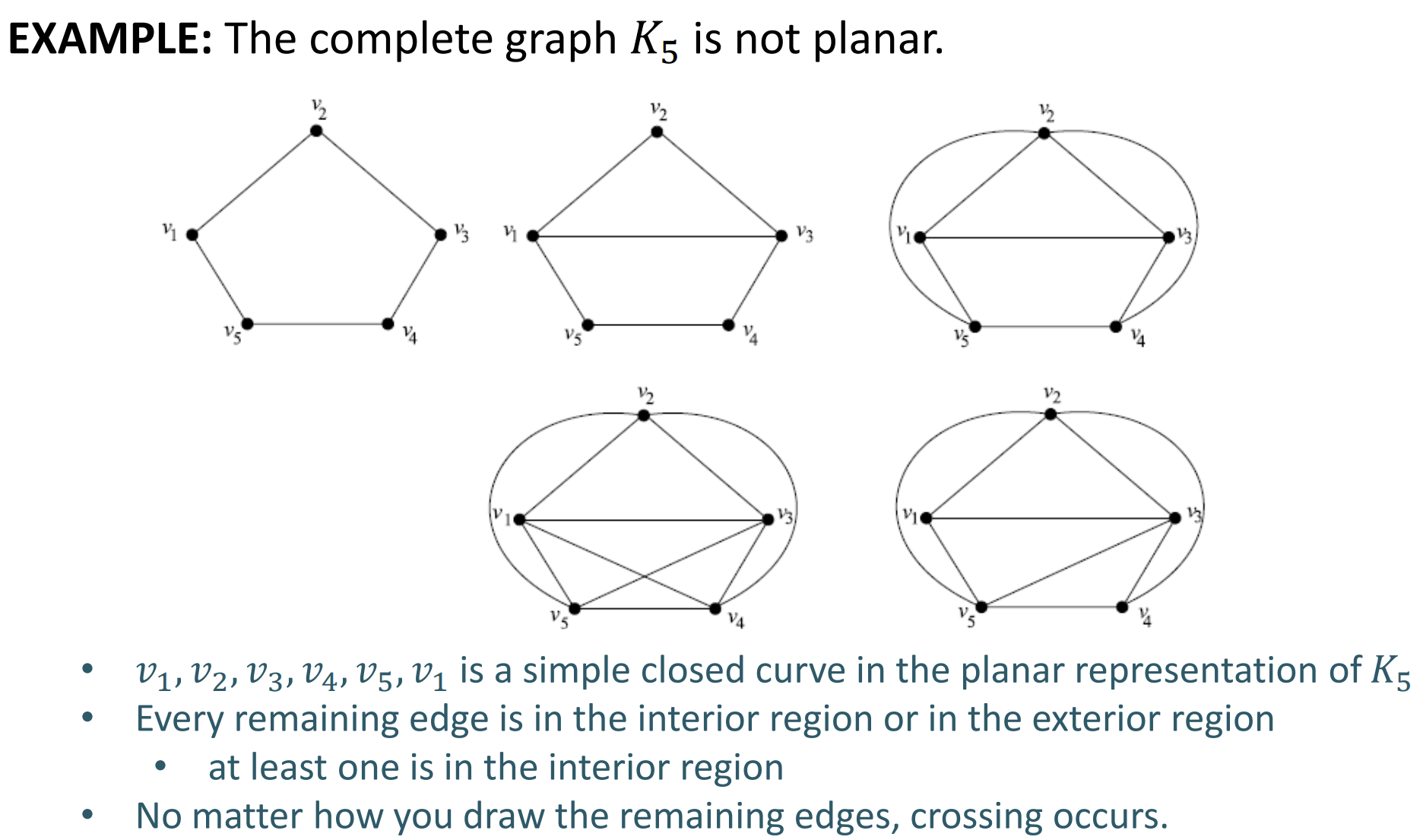
非平面图 - Nonplaner Graph

• Jordan曲线定理: 如果有一个闭合曲线, 那么这个闭合曲线必然会把所处的平面分成两个区域. 任何连接这两个区域的曲线都会与原来的曲线交叉.

• e.g. $K_{3,3}$不是平面图

  • 

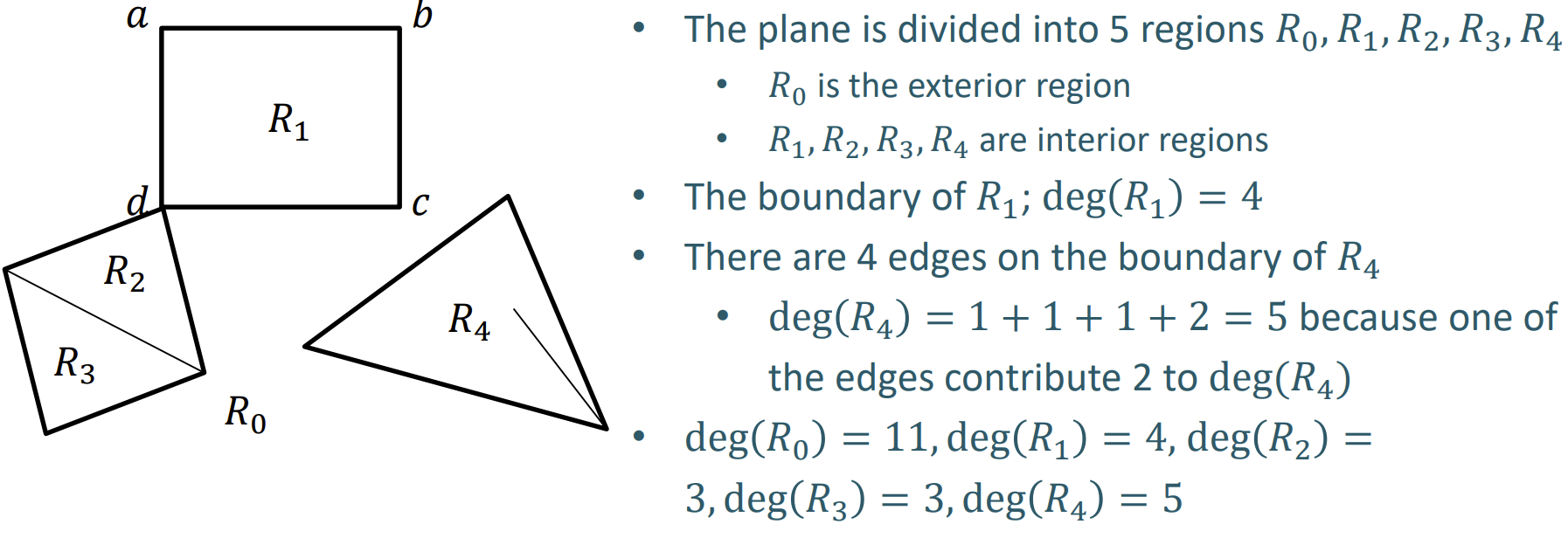
欧拉公式 - Euler’s Formula

区域 - Region

一个闭合曲线将空间分成几个区域.

• 度:
  • 这个区域由多少遍围成的.
  • 如果有一条孤立的边, 那么这条边对度数的贡献为2
• 外部面: 无穷的空间(曲线围成的区域外部)
• 内部面: 有限的区域空间(曲线围成的区域)

欧拉公式

$V+F=E+2$

应用

• 定理: 令图$G$是一个连接平面上的简单图, 如果每个面$R_i$都有$\mathrm{deg}(R_i)\ge l$, 那么$|E(G)|\le \frac{l}{l-2}(|V|-2)$
• 推论: 令图$G$是一个连接平面上的简单图, 那么一定有$|E(G)|\le 3|V|-6$
• e.g. $K_5$不是平面图
  • $|E(K_5)|=C_5^2=10,|V(K_5)|=5\therefore |E(K_5)|\ge 3|V(K_5)|-6\therefore$不是平面图

同胚 - Homeomorphic

• 定义: 在同一个初始图上初等细分之后得到的图是同胚的.
• 初等细分 - elementary subdivision: 在一条边上加上一个顶点.

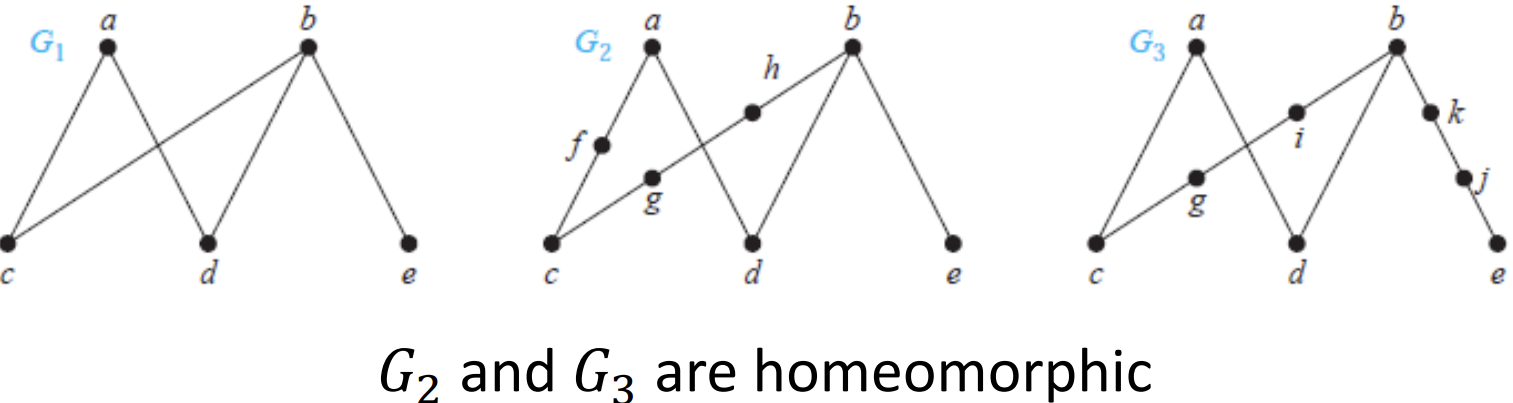
Kuratowski定理

• 定义: 一个非平面图一定是与$K_{3,3}$或者$K_5$同胚

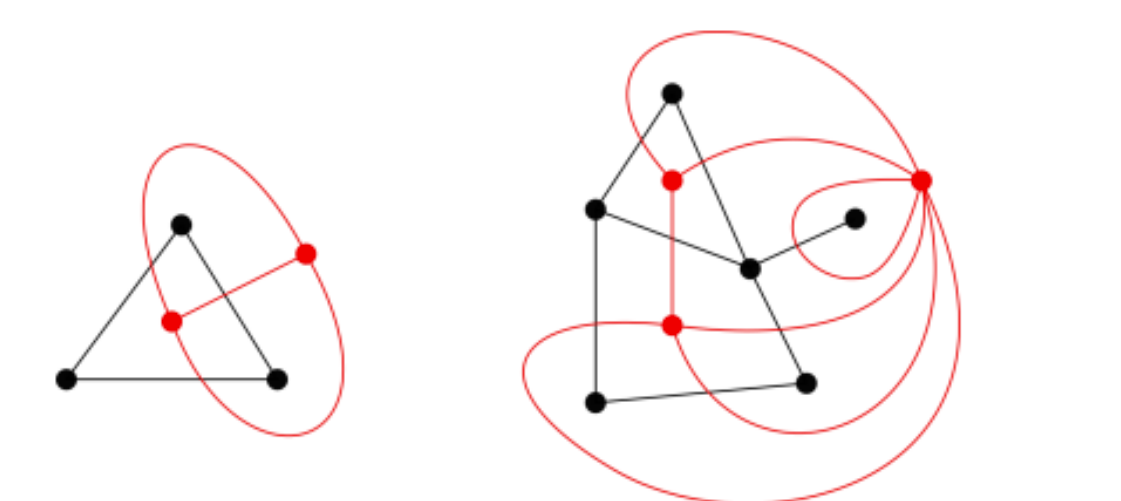
对偶图 - Dual Graph

在每一个区域连一个点, 然后在每一个公共边处连一条线(连接区域对应的点), 得到的图

五色定理 - 5-coloring Theorem

• 定理: 最多用五种颜色可以把一个平面图的所有区域染上色.

四色定理

略

树 - Tree

• 定义: 连接无向无环图
• 森林: 多棵树组成的图

性质:

• 定理: 每两个顶点之间有且仅有一条简单的路径.(如果有多条路径, 那么一定有环, 与树的定义冲突)
• 边: n-顶点的图有$n-1$条边. (数学归纳法: 假设$k$顶点有$k-1$边, $k+1$顶点多了一个顶点, 用一条边链接, 那么边是$k$, 得证)
• 树是连接的

上述三点知二推一, 或者说知道两点就能判断是一颗树.

子节点不超过m的树被称作m叉树(m-ary)

平衡树 - Balance Tree

• 定义: 一颗$m$叉树所有的叶节点都是在$h$层或者$h-1$层的时候被称为平衡树

• 定理: $h$层的$m$叉树最多有$m^h$个叶节点

• 推论: $m$叉树有$h$层$l$个叶节点, 那么$h\ge \lceil {\log }_{m}l\rceil$. 如果是全满且平衡的m叉树, 那么$h=\lceil {\log }_{m}l\rceil$

叶节点只是一个分支的最底层的节点(就是最子的节点)

树的遍历 - Tree Traversal

把节点全走一边

遍历

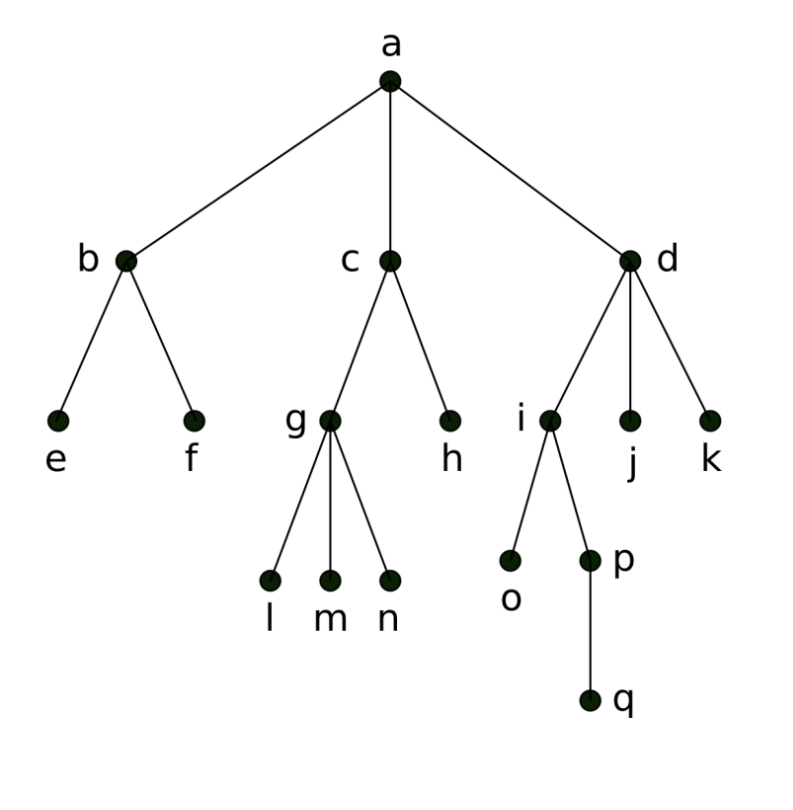
1. 先序遍历 - Preorder

   

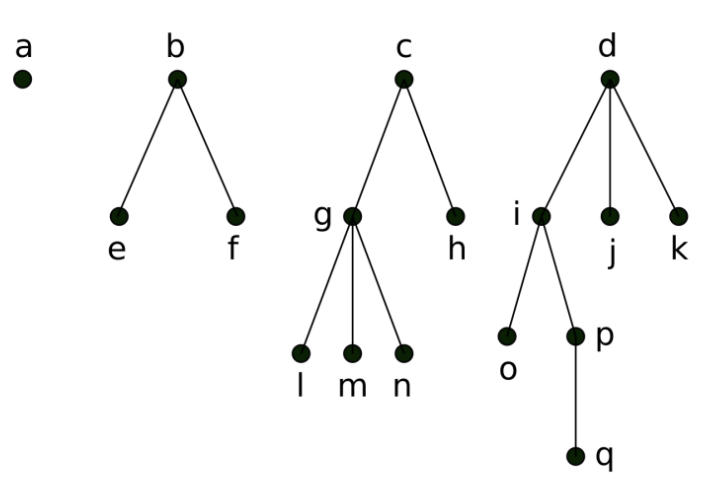
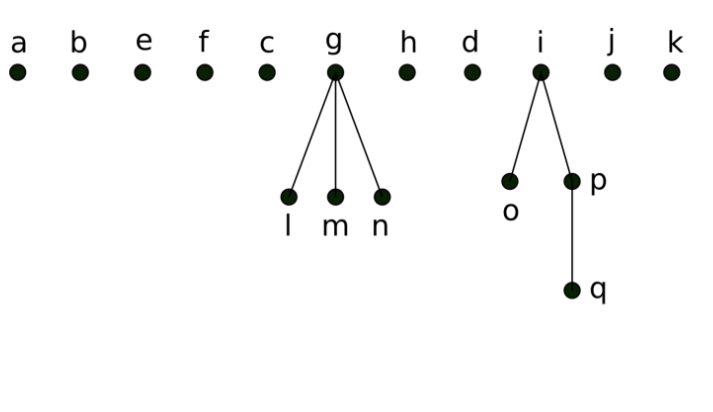
2. 中序遍历 - Inorder

   从左边最深的节点(叶节点)开始, 遍历到上一层, 查找该层是否有其他子节点, 如果有, 再从左往右找叶节点开始遍历, 如果全遍历完, 去找父节点, 重复上述过程.

   $e\to b\to f\to a\to l\to g\to m\to n\to c\to h\to o\to i\to q\to p\to d\to j\to k$

3. 后序遍历 - Postorder

   从左往右, 从下往上

   $e\to f\to b\to l\to m\to n\to g\to h\to c\to o\to q\to p\to i\to j\to k\to d\to a$

深度优先搜索 - DFS Depth First Search

一般用递归

广度优先搜索 - BFS Breadth First Search

一般用栈

生成树 - Spanning Tree

• 定义: 一个简单图中的子图, 且这个子图是一颗包含这个简单图所有节点的树.

• 定理: 如果一个简单图连接$\iff$有生成树(当且仅当, 互推)

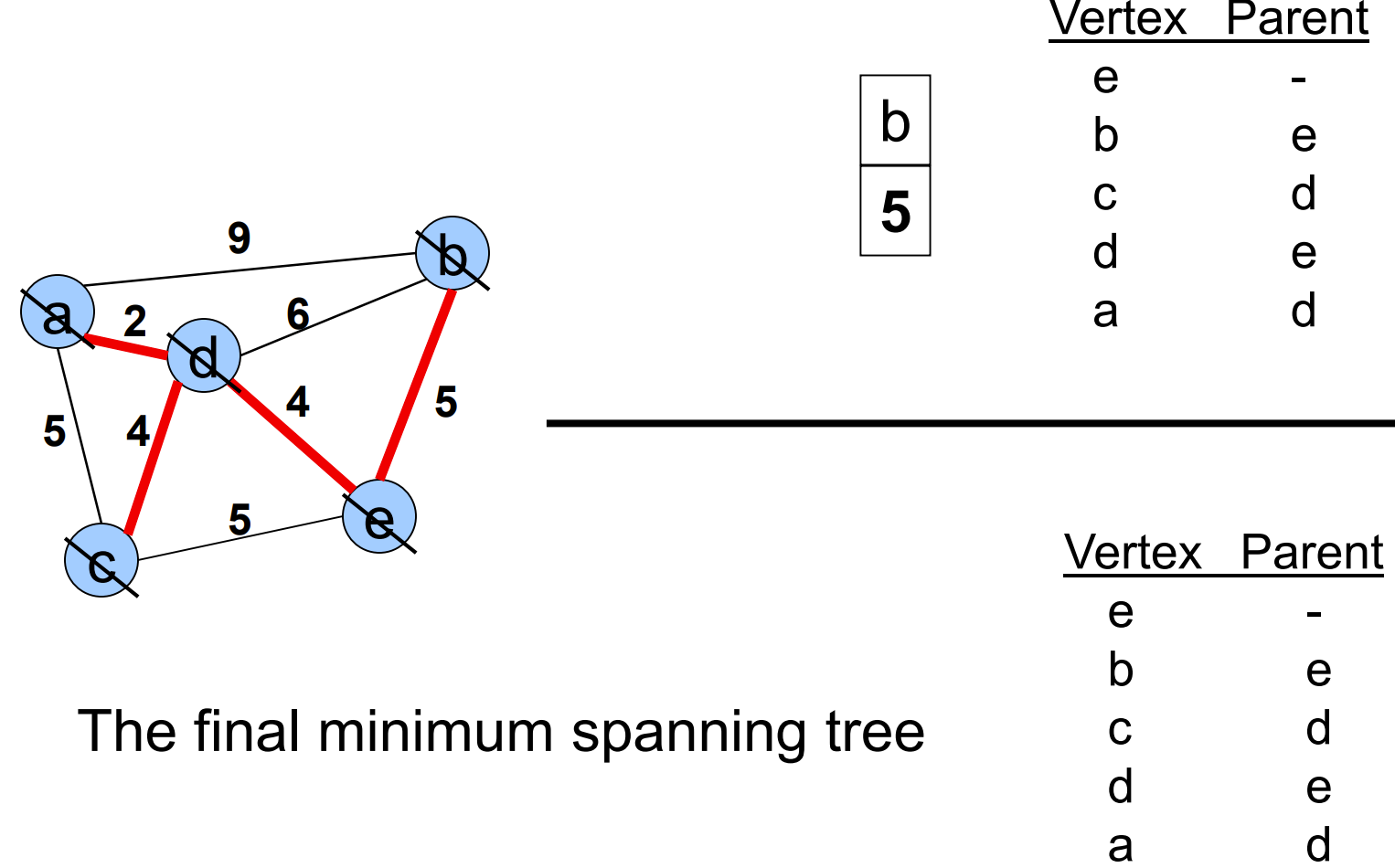
最小生成树 - Minimum Spanning Tree(MST)

• 定义:
  • 是一棵树
  • 遍历所有顶点
  • 在所有生成树中, 边的权重之和最小
  • 不一定是唯一的

Prim算法

组合数学

前置知识

函数与集合 - set and function

1. injection单射: $a\ne b\Rightarrow f(a)\ne f(b)$, 或$f(a)=f(b)\Rightarrow a=b$
2. surjection满射: $\forall b\in B,\exists a\in A,f(a)=b$
3. bijection双射: 同时满足双射和单射

基数 - Cardinality

定义1: 令$A$是一个集合, 如果$A$有可数的元素个数, 那么$A$是可数集(finite set). 否则, $A$是无限集(infinite set)

定义: 一个可数集$A$中的基数$|A|$就是$A$中元素的个数.

定义:

1. $|A|=|B|\iff f:A\to B$ 是一个双射
2. $|A|\le |B|\Leftarrow f:A\to B$ 是一个单射
3. $|A|\le |B|\Leftarrow f:A\to B$ 是一个单射, 但是不是一个满射

定理: $|A|=|B|,|B|=|C|\Leftarrow |A|=|C|$

例子: $|{\mathbb{Z}}^{+}|=|\mathbb{N}|=|\mathbb{Q}|=|{\mathbb{Q}}^{+}|=|\mathbb{Z}|$, $|\mathbb{R}|=|{\mathbb{R}}^{+}|=|(0,1)|=|[0,1]|$

可列和不可列 - Countable and Uncountable

定义: 如果$|A|<\infty$或者$|A|=|mathbbZ|$, 那么$A$是可列的. 否则, $A$是不可列的

Schroder-Bernstein Theorem

用于比较两集合的基数.

定理: $|A|\ge |B|,|B|\ge |A|\iff |A|=|B|$, 这里可以用单射证明